Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 43
Determine os valores máximo e mínimo absolutos da função e identifique onde ocorrem.
Passo 1
Para determinar os valores máximo e mínimo absolutos, podemos fazer a derivada da função dada e igualar este resultado a zero (encontrar ponto(s) crítico(s)). Fazendo esse procedimento, temos que:
A primeira derivada da função fornecida, depois que igualada a zero, tem como solução, ou seja, esse é o ponto crítico a ser avaliado.
Para , é positivo;
Para , é positivo.
Com isso, não é possível tirar uma conclusão em relação a esse ponto.
Passo 2
Para facilitar a análise dos pontos, podemos criar a curva do gráfico da função dada.
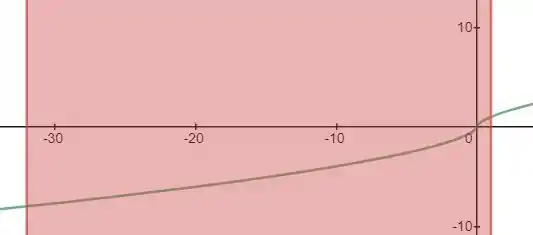
Observando o desenho feito do gráfico, pode-se concluir que a função é crescente em .
Como o intervalo dado é fechado, além do ponto crítico encontrado, podemos analisar os pontos dos limites laterais do mesmo e descobrir suas coordenadas. Assim, temos:
Passo 3
A partir do resultado da função em cada ponto avaliado, conclui-se que o máximo absoluto é e o mínimo absoluto é .
Resposta
Máximo absoluto: em ;
Mínimo absoluto: em .