Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.3 - Ex. 45
45. Ache uma equação de cada uma das retas que passam pelo ponto (4,13), que sejam tangentes à curva .
Passo 1
Foi nos dado a curva.e um ponto P= (4,13)
Inicialmente vamos verificar se esse ponto pertence a curva:
.
.
Substituimos as coordenadas do Ponto na equação da curva e a igualdade não foi satisfeita. Então, o ponto não pertence a curva.
Um esboço bem simplificado do que está acotecendo:
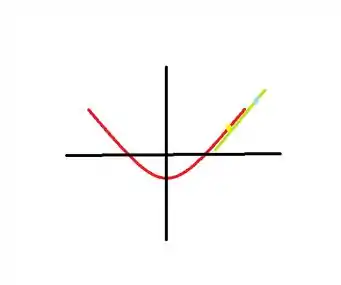
O que queriamos é o ponto amarelo, um ponto que está tanto na curva como na reta tangente. Mas o que temos é o ponto azul, que está só na reta tangente. Então, nossa missão inicial é encontrar esse ponto presente tanto na curva como na reta.
Passo 2
Derivando a função:
Passo 3
Equação da reta tangente:
Lembrando que esse e são as coordenadas do ponto que estão na reta tangente.
Então, substituindo o que temos na equação:
Lembre o que estamos procurando, um ponto que esteja tanto na reta como na curva, logo, pelo menos um y da curva deve satisfazer a equação da reta:
Resolvendo por bhaskara, encontraremos duas raízes: x=1 e x=7. Agora sim podemos calcular a inclinação da reta tangente.
Para x=1
Para x=7
Passo 4
Portanto, as equações da reta tangente serão:
E