Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.6 - Ex. 45

45-48. Esboce a regra descrita e encontre sua área.

45. A região abaixo da curva y = x 2 + 1 e acima do intervalo 0 ,   3 .

Passo 1

Então pessoal, inicialmente o que temos que fazer é esboçar a curva em questão, ok? Esboçando a curva que nos foi dada, teremos:

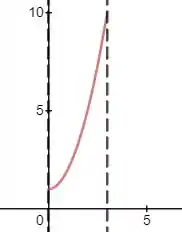
O que queremos calcular aqui é essa região abaixo da curva em vermelho, limitada pelo intervalo 0 ,   3 , que são as retas pontilhadas! Tendo isso em vista, então bora pra cima!

Passo 2

Escrevendo a integral dessa área:

∫ 0 3 x 2 + 1 d x

Simplificando:

∫ 0 3 x 2 d x + ∫ 0 3 1 d x

Para resolvermos essas integrais devemos utilizar a seguinte regrinha:

∫ x n d x = x n + 1 n + 1

Para a primeira integral, teremos:

∫ 0 3 x 2 d x = x 3 3 3 0

Para a segunda integral, teremos:

∫ 0 3 1 d x = x 3 0

Logo:

∫ 0 3 x 2 + 1 d x = x 3 3 3 0 + x 3 0

Passo 3

Agora que resolvemos nossa integral, basta que apliquemos o Teorema Fundamental do Cálculo (Parte 1) para eliminarmos os intervalos de integração, saca só:

∫ 0 3 x 2 + 1 d x = 27 3 + 3

∫ 0 3 x 2 + 1 d x = 12

∴ A = 12   u . a

E esse é o valor da nossa região! 😉

Resposta

A = 12   u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13-30. Calcule a integral usando a Parte 1 do Teorema Fundamental do Cálculo.24. ∫ 1 2 1 1 2 x d x
31-34. Use o Teorema 5.5.5 para calcular as integrais dadas.33. a) ∫ - 1 1 e x - 1 d x
35-36. É dada uma função f x definida por partes num intervalo. Nestes exercícios: a) use o Teorema 5.5.5 para encontrar a integral de f x no intervlao; b) encontre uma antiderivada de f x no interval
31-34. Use o Teorema 5.5.5 para calcular as integrais dadas.34. a) ∫ - 3 3 x 2 - 1 - 15 x 2 + 1 d x
13-30. Calcule a integral usando a Parte 1 do Teorema Fundamental do Cálculo.27. ∫ 2 2 d x x x 2 - 1