Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.6 - Ex. 50
49-52. Esboce a curva e encontre a área total entre a curva e o intervalo dado do eixo .
50.
Passo 1
Então pessoal, antes de escrevermos a integral que temos que calcular vamos esboçar a curva que nos foi dada, tudo bem? Vale lembrar que a curva tem um intervalo, então é limitada! A curva que nos foi dada é:
E o intervalo é: . Esboçando a região:
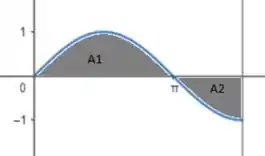
Note que temos duas áreas: e . Sendo assim, teremos as seguintes integrais para resolver:
Logo:
Então vamo que vamo!
Passo 2
Vale ressaltar que as integrais que escrevemos possuem o mesmo integrando, então o resultado de uma será o mesmo da outra, o que poupa nosso tempo! De acordo com o que estudamos em derivadas a função que quando derivada resulta em é , logo:
Agora que resolvemos as integrais, basta que apliquemos o Teorema Fundamental do Cálculo (Parte 1) para eliminarmos os intervalos de integração, saca só:
E esse é o nosso resultado, galera!