Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.7 - Ex. 49
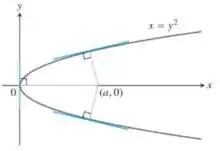
49. Mostre que se é possível desenhar três normais a partir do ponto até a parábola , apresentada no driagrama a seguir; então deve ser maior que . Uma das normais é o eixo . Para que valor de as outras duas normais são perpendiculares?
Passo 1
Como comentado na seção 7 do George, sabemos que a reta normal é a reta perpendicular àquela que tangencia a curva no ponto de incidência. Dessa forma, antes de tudo devemos derivar implicitamente a equação que nos foi dada. Fazendo isso, teremos:
Passo 2
Nosso objetivo agora é encontrar a reta que tangencia a curva, ou seja, a derivada da equação no ponto que foi dado, que é . No entanto, de forma genérica, precisamos de dois pontos para determinar a equação da reta. Dessa forma, teremos: .
Isolando , teremos:
Passo 3
Pela simetria da parábola que nos foi dada, temos que os pontos no qual se encontram as retas normais são:
Se as duas retas são perpendiculares, então o produto entre elas tem que ser . Logo:
Lembrando que os pontos foram aplicados na equação da reta também, ok? Continuando, temos:
Passo 4
De acordo com os pontos que comentamos no passo anterior, , então se , isso implica que , certo?
Substituindo os valores de e na equação:, então conseguiremos descobrir o valor de .
Para , temos:
Para , temos:
Sendo assim, fica provado que , c.q.d.
Resposta
Ei, a resposta está no passo a passo :)