Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.5 - Ex. 51
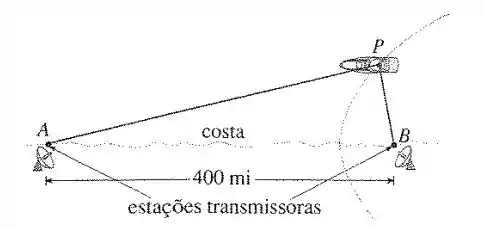
51- No sistema de navegação LORAN (LOng RAnge Navigation), duas estações de rádio localizadas em e transmitem simultaneamente sinais para um barco ou um avião localizado em . O computador de bordo converte a diferença de tempo na recepção desses sinais em diferença de distância e isso, de acordo com a definição de uma hipérbole, localiza o navio ou avião em um ramo da hipérbole (veja a figura). Suponha que a estação esteja localizada a leste da estação na costa. Um navio recebe o sinal de microssegundos antes de receber o sinal de .
- Assumindo que o sinal de rádio viaja a uma velocidade de , encontre uma equação da hipérbole na qual o navio esteja.
- Se o navio for esperado ao norte de , a que distância da costa estará o navio?
Passo 1
Olá, meu amigo. Vamos resolver juntos essa atividade aqui. A gente tem duas estações de rádio, e e elas transmitem um sinal para , utilizando a equação geral da hipérbole:
Conseguiremos encontrar a localização do navio em . Veja abaixo que:
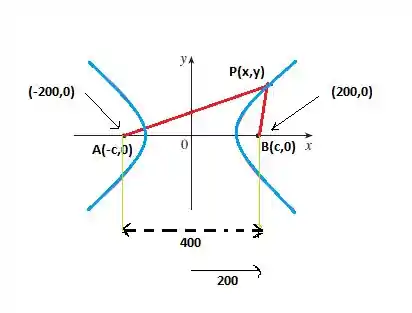
A gente vai utilizar a definição da hipérbole, sendo assim:
Vamos também utilizar da velocidade dada na letra a, ela será utilizada para encontrar essa distancia acima.
Na letra b, a gente vai utilizar a equação que encontrarmos na letra a, e iremos utilizar da informação que se o navio está diretamente ao norte de , então a coordenada do navio é a mesma que a coordenada de , que é milhas.
Passo 2
Vamos facilitar a nossa vida e considerar que o centro está na origem da equa��ão dessa hipérbole e que ela está no ponto médio da reta indo de para ou seja.
O que nos dá um valor de igual a
Então pela definição de hipérbole temos:
Onde a distância é a distância relativa dada pela diferença de tempo de um sinal para o outro ou seja:
O sinal aqui não importa, o que importa é a distância relativa.
A conversão pés para milhas é dada por:
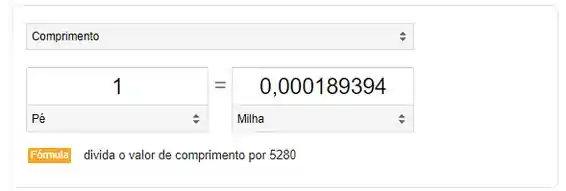
Logo:
Logo:
Passo 3
Com os valores de e de temos o valor de :
Pela hipérbole estar com os focos em uma reta horizontal teremos então a seguinte equação para ela:
Logo a resposta da letra a será:
Passo 4
Quando se diz que o navio estará a norte de quer dizer o navio estará na mesma posição do radar em porém não sabemos a posição em que dita o norte tal como no desenho abaixo.
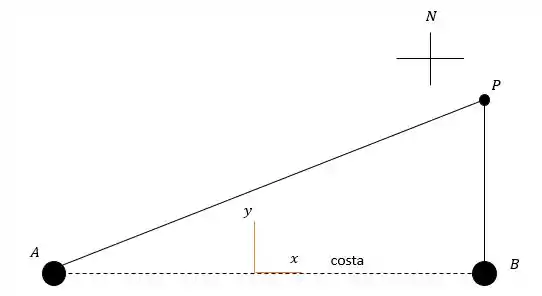
Logo então: