Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.5 - Ex. 48

Encontre uma equação para a cônica que satisfaça as condições dadas.

48-

Hipérbole, focos ( 2,2 ) e ( 6,2 ) assíntotas y = x - 2 e y = 6 - x

Passo 1

Olá, meu querido e nobre amigo. Deveremos encontrar a equação da hipérbole aqui.

Ela deve ter os focos em:

2,2   ; 6,2

E assíntotas em:

y = x - 2

y = 6 - x

Pelos pontos dos focos estarem na reta igual a y = 2 , ou seja numa reta horizontal quer dizer que nós temos uma hipérbole horizontal de equação igual a:

( x - x 0 ) 2 a 2 - ( y - y 0 ) 2 b 2 = 1

E que o centro dessa hipérbole estará em uma posição igual a:

x 0 , y 0 = 2 + 6 2 , 2 = ( 4,2 )

O centro, é o ponto médio do foco. Logo c = 2 .

Pois:

P o n t o s   d e   f o c o = ( 4 ± c , 2 )

Então as assíntotas terão a seguinte cara:

y - y 0 = ± b a ( x - x 0 )

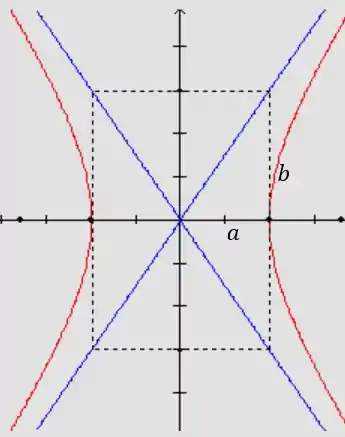
Passo 2

Então vamos organizar as assíntotas dadas para que tenhamos uma forma de dizer quem é a e b .

Primeiramente por ser uma hipérbole:

c 2 = a 2 + b 2

a 2 = 4 - b 2

Agora abrindo:

y - y 0 = ± b a ( x - x 0 )

Substituindo os valores que a gente já tem:

y - 2 = ± ( x - 4 )

Como nossas assíntotas são:

y = x - 2   ;   y = 6 - x

Com o resultado que encontramos da equação da assíntota generalizada conseguimos dizer que:

b a = 1

b = a

Logo:

a 2 = 4 - a 2

a 2 = b 2 = 2

Logo a equação da hipérbole fica da seguinte forma:

( x - 4 ) 2 2 - ( y - 2 ) 2 2 = 1

Resposta

( x - 4 ) 2 2 - ( y - 2 ) 2 2 = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça um esboço da parábola com equação y = x 2 - 8 x . Ache (a) o vértice, (b) a equação do eixo, (c) o foco e (d) a equação da diretriz.
Dada a parábola com equação y 2 + 8 x - 6 y = 7 , ache (a) o vértice, (b) a equação do eixo, (c) o foco e (d) a equação da diretriz. Faça um esboço da curva.
Nos exercícios de 1 a 4, (a) ache a equação da parábola tendo o foco e a diretriz dados, (b) ache o comprimento do latus rectum e (c) faça um esboço da parábola.1.Foco em ( 0 ,- 3 ) ; diretriz, y = 3
Nos exercícios de 1 a 4, (a) ache a equação da parábola tendo o foco e a diretriz dados, (b) ache o comprimento do latus rectum e (c) faça um esboço da parábola.2.Foco em ( 0 ,4 ) ; diretriz, y = - 4
Encontre o vértice, o foco e a diretriz da parábola e esboce seu gráfico. 3 x 2 + 8 y = 0