Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.5 - Ex. 53

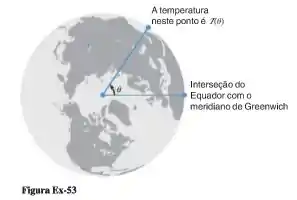
53- Prove que existem pontos diametralmente opostos no Equador terrestre em que se registra a mesma temperatura.[Sugestão: Considere a figura dada, em que aparece o Equador visto de algum ponto acima do Polo Norte. Suponha a temperatura seja uma função contínua do ângulo e considere a função

Passo 1

Galerinhaaa, primeiro vamos entender o que nós temos que provar para satisfazer a questão.

Cara, é a temperatura de um lado e é a temperatura do outro lado do equador, Ok ?

Bom, nós temos que provar que existe um que zere a nossa função e, com isso:

Sacou ?!

Passo 2

Nós temos que:

Substituindo na primeira função: (lembrando que: )

Com isso,nós podemos afirmar que se . Do mesmo jeito, se .

Dessa forma, pelo Teorema do Valor Intermediário, existe um , tal que , já que é contínua no intervalo e tem sinais opostos e são diferentes de zero. Isso que dizer que temos:

Fala sério, achou que ia ser mais difícil, né ?!

Resposta

Demonstração acima.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1-4. Seja f a função cujo gráfico é dado. Em quais (se houver) dos intervalos seguintes f é contínua?1. a) [ 1 ,3 ] b) ( 1 ,3 ) c) [ 1 ,2 ] d) ( 1 ,2 ) e) [ 2 ,3 ] f) ( 2 ,3 )

1-4. Seja f a função cujo gráfico é dado. Em quais (se houver) dos intervalos seguintes f é contínua?2. a) [ 1 ,3 ] b) ( 1 ,3 ) c) [ 1 ,2 ] d) ( 1 ,2 ) e) [ 2 ,3 ] f) ( 2 ,3 )

39- Prove que f x = x 3 5 é contínua em toda parte, justificando cuidadosamente cada passo.

45-Dê um exemplo de uma função que está definida em todo ponto de um intervalo fechado e cujos valores nas extremidades têm sinais opostos, mas para a qual a equação f x = 0 não tem solução no interva

33-34 Diz-se que uma função f tem descontinuidade removível em x = c se lim x → c ⁡ f ( x ) existe mas f não é contínua em x = c ou porque f não está definida em c ou porque a definição de f ( c ) dif