54-Seja R uma região elíptica no plano x y e defina f ( z ) como a área da parte de R que está sobre à esquerda da reta vertical x = y . Prove que f é uma função contínua de z .[Sugestão: Suponha que a elipse esteja localizada entre as retas horizontais y = a e y = b , ab . Convença-se de que f z 1 - f ( z 2 ) ≤ b - a . z 1 - z 2 .]

Enunciado

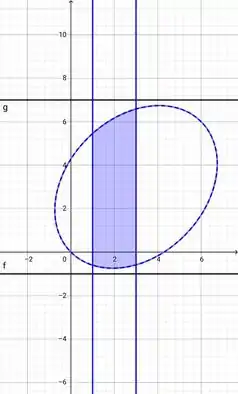
Galerinha, vamos combinar uma coisa, ok?

é a área pintada em azul (não sei se é azul mesmo, mas a gente finge que é);

As restas e são respectivamente, e ;

A área em azul (?) é menor que a área do retângulo: .

Assim,

Sem considerar necessariamente , temos:

Com isso, dá pra mostrar que é contínua.

Como:

Pelo Teorema do Confronto:

Agora, nós temos que:

Amíguineos, percebam que aqui nós consideramos que um número é menor ou igual ao seu módulo e maior ou igual a menos o seu módulo.

Como,

De novo pelo Teorema do Confronto nós temos que:

Com isso,

Como podem ser quaisquer valores e, , em , nós provamos que é contínua em qualquer .

Fim!

Demonstração acima.