Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.5 - Ex. 34

34- a) A terminologia descontinuidade removível é apropriada porque uma descontinuidade removível de uma função f   em um ponto x = c pode ser “ removida”, redefinindo o valor de f apropriadamente em x = c . Que valor de f ( c ) remove a descontinuidade ?

b)Mostre que as seguintes funções tem descontinuidade removível em x = 1 e esboce seus gráfico.

f x = x 2 - 1 x - 1

g x = 1 ,   x > 1 0 ,   x = 1 1 ,   x < 1

c)Quais valores de f ( 1 ) e g ( 1 ) removem as descontinuidades ?

Passo 1

a)Galera, um a função tem uma descontinuidade removível em x = c , se lim x → c ⁡ f ( x ) existe, mas f não é contínua em x = c . Dessa forma, se tivermos lim x → c ⁡ f ( x ) = f ( c ) , nós poderemos remover a descontinuidade.

Passo 2

b) Galerisss, para nós sabermos se as funções tem descontinuidade removível em x = 1 , nós temos temos que checar se os limites delas existem, quando x → 1 , fechou ?! Então, vamos lá!

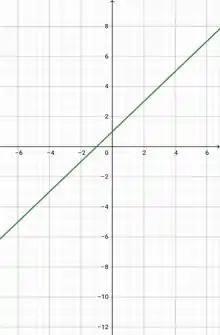
Para f ( x ) :

lim x → 1 ⁡ x 2 - 1 x - 1

Abrindo o numerador:

lim x → 1 ⁡ x - 1 × x + 1 x - 1

Dessa forma,

lim x → 1 ⁡ x + 1 = 2

Temos o seguinte gráfico para f ( x ) :

Para g ( x ) :

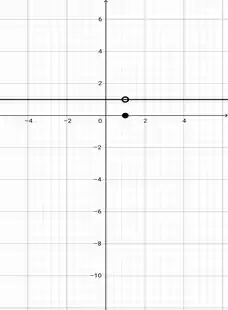
Bom, como nós temos um função partida, o valor de lim x → 1 + ⁡ g x = lim x → 1 - ⁡ g x , sacou ???

Só de olharmos a função nós já percebemos que lim x → 1 + ⁡ g x = lim x → 1 - ⁡ g x = 1 .

Temos os seguinte gráfico para g ( x ) :

Passo 3

c)Como o único jeito de remover a descontinuidade é que:

f 1 = lim x → 1 ⁡ f ( x )

Então, f 1 = 2 .

Da mesma forma,

g 1 = lim x → 1 ⁡ g ( x )

Logo, g x = 1

Resposta

  1. lim x → c ⁡ f ( x ) = f ( c ) .
  2. lim x → 1 ⁡ f ( x ) = 2 , lim x → 1 ⁡ g ( x ) = 1 . Como os limites das duas funções existem, ambas possuem descontinuidade removível.
  3. f 1 = 2 e g 1 = 1
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Construa o gráfico e analise a continuidade das seguintes funções: f x = ln ⁡ x + 1 , x ≥ 0 - x, x0
Determine, se existirem, os pontos onde as seguintes funções não são contínuas. f x = x x - 3 x + 7
Investigue a continuidade nos pontos indicados: f x = x 2 sen ⁡ 1 x ,x ≠ 0 0 ,x = 0e mx = 0
Sejam a ∈ R e f : R → R uma função definida no ponto a . Se lim x → a ⁡ f x - f a x - a = m , prove que f é contínua no ponto a .
Defina funções f , g e h que satisfaçam: f não é contínua em 2 pontos de seu domínio; g é contínua em todos os pontos de seu domínio mas não é contínua em R ; h ∘ f é contínua em todos os pontos do do