Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 58
(a) Demonstre que a equação tem pelo menos uma raiz real.
(b) Use sua calculadora para encontrar um intervalo de comprimento que contenha uma raiz.
Passo 1
Fala, gente bonita! Tudo certinho com vocês?
Essa questão pede pra mostrarmos que existe pelo menos uma raiz real nessa equação aqui:
De maneira geral, como não precisamos descobrir qual é a raiz e apenas queremos mostrar que ela existe, a nossa melhor aposta vai ser o Teorema do Valor Intermediário. Já já vamos ver como fazer isso!
Além disso, a questão pede pra usarmos uma calculadora pra encontrarmos um intervalo de comprimento que contenha a raiz. Vamos precisar testar alguns valores na calculadora pra isso.
Vem com a gente!
Passo 2
A melhor maneira de usar o Teorema do Valor Intermediário é ter uma equação com um em um dos lados. Então vamos fazer isso na nossa equação:
Agora vamos definir a função:
A ideia pra provarmos que tem uma raiz vai ser basicamente o seguinte:
Provar que a função é continua num intervalo
Achar dois pontos tal que o e
Se conseguirmos usar o Teorema do Valor Intermediário pra provar que é igual a pra algum valor de , mostramos que existe raiz na nossa equação inicial. Pegou a ideia?
Vamos lá!
Passo 3
Em primeiro lugar, precisamos lembrar que o Teorema do Valor Intermediário só é válido pra funções contínuas. Então precisamos checar se é contínua.
Uma das formas de provarmos isso é lembrando que se e forem contínuas, então também é contínua.
Podemos afirmar diretamente que é contínua em todo o seu domínio, pois se trata de uma função logarítmica. O mesmo vale pra , pois se trata de uma função polinomial. Logo, podemos dizer que a função também é contínua em todo o seu domínio.
Passo 4
Agora que sabemos que a nossa função é contínua, basta achar um valor de positivo e um negativo, pois assim, garantirmos que a curva irá cruzar o eixo , portanto, uma raiz. Olha só uma ilustração desse lance de cruzar o eixo :
Vamos ver
Para :
Achamos um valor negativo, agora basta acharmos um positivo.
Para :
Pelo Teorema do Valor Intermediário, vemos que existe pelo menos uma raiz entre os pontos e .
Boa! Partiu próximo!
Passo 5
(b) Esse item é tentativa e erro. Usando uma calculadora vemos o seguinte:
Podemos tentar esboçar um gráfico para facilitar, olha só:
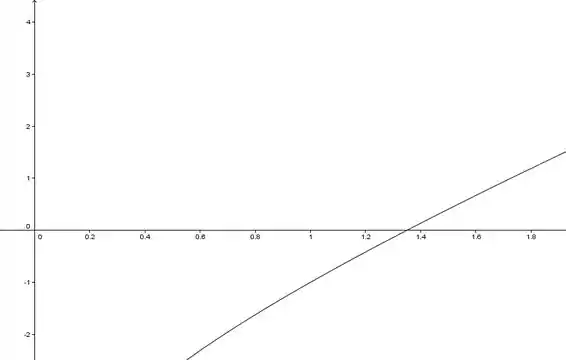
Para :
Para :
Ainda negativo. Estamos perto, mas precisamos aumentar um pouco mais o valor de :
Para :
Estamos perto! Só mais um pouquinho agora:
E para :
Opa, achamos um valor positivo de e um valor negativo de tal que . Dessa maneira, o intervalo é:
Resposta
a) Resposta no texto
b)