Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.5 - Ex. 6
Esboce o gráfico de uma função que tenha uma descontinuidade de salto em e uma descontinuidade removível em , mas seja contínua no restante.
Passo 1
Olá, vamos para mais essa resolução?
Então, a gente tem aqui uma atividade que nos pede para desenharmos o gráfico de uma função que contenha uma descontinuidade de salto no ponto e uma descontinuidade removível em .
É importante deixar claro que não é necessário escrever uma expressão matemática para a função, o enunciado pede apenas um esboço de um gráfico.
Uma descontinuidade de salto é do tipo:
Uma descontinuidade de salto ocorre em uma função quando há uma mudança abrupta no valor da função em um ponto específico. Essa mudança é como um "salto" na função quando você passa por esse ponto.
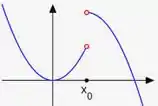
Uma descontinuidade removível aparece quando os limites laterais à direita e à esquerda são iguais entre si, porém diferentes do valor da função. Graficamente ele se apresenta assim:
Passo 2
Considerando a função constante, é simples construir a função que tem uma descontinuidade no ponto dado . Por exemplo, podemos usar a função
Podemos concluir que é contínua nos intervalos e . Uma vez que tem os valores constantes à esquerda de com valor e à direita de com valor , temos que
Os limites e são distintos, então a função dada tem uma descontinuidade de salto em , mas é contínua em e este é o problema. Portanto, precisamos fazer alguma modificação nesta função. Talvez a maneira mais fácil de obter a descontinuidade removível em seja usar o ponto e movê-lo para algum outro ponto na linha . Esta é a abordagem geométrica e é necessário nos inspirar para construir a função
Uma vez que tem os valores constantes à esquerda de com valor e à direita de com valor , temos que
O resultado implica que existe e é igual a , mas não é igual a , então a função dada tem a descontinuidade removível em . Portanto, a função satisfaz a condição dada e seu gráfico é dado na figura abaixo.
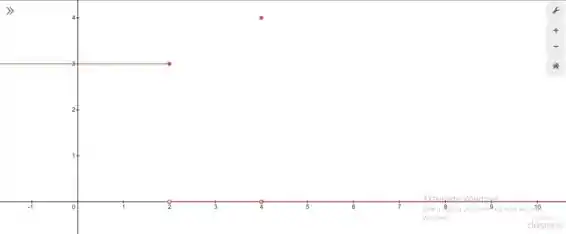
Resposta
