Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 2
Se é contínua em , o que você pode dizer sobre seu gráfico?
Passo 1
Fala galera!!! Essa é uma questão puramente conceitual que cobra o conhecimento do aluno sobre como é o gráfico de uma função contínua.
Ela quer saber qual o comportamento de um gráfico de uma função continua.
Passo 2
Bom, uma função é contínua em determinado ponto se o limite dessa função quando tender a esse ponto for igual ao valor da função neste ponto. Se a função for contínua na reta real toda, isto é, no intervalo , então em todos os pontos o limite será igual ao valor da função.
A consequência imediata disso é que o gráfico da função não terá saltos ou buracos, e também não terá ‘quinas’, em outras palavras, se alguém for desenhar a curva que descreve a função com uma caneta num papel, não será necessário tirar a caneta do contato com o papel em nenhum momento!!!
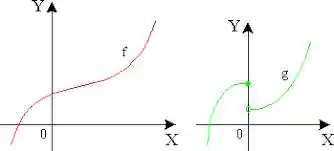
Na figura ilustramos em vermelho uma função contínua na reta real toda e em verde uma função descontínua em um ponto:
Resposta
R: Sendo a função contínua na reta real inteira, seu gráfico será uma curva sem saltos ou buracos.