Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 60
60. Como tossimos.
a. Quando tossimos, a traqueia se contrai e aumenta a velocidade do ar que passa. Isso levanta questões sobre quanto ela deveria se contrair para maximizar a velocidade e se ela realmente se contrai tanto assim quando tossimos. Considerando algumas hipóteses razoáveis sobre a elasticidade da traqueia e de como a velocidade do ar próximo às paredes é reduzida pelo atrito, a velocidade média do fluxo de ar pode ser modelada pela equação:
onde é o raio, em centímetros, da traqueia em repouso e é uma constante positiva, cujo valor depende em parte do comprimento da traqueia.
Demonstre que é máximo quando ; ou seja, quando a traqueia está contraída em cerca de . O impressionante é que imagens obtidas com raios X confirmam que a traqueia se contrai nessa proporção durante a tosse.
b. Sendo e , trace o gráfico de no intervalo . Compare o que você observa com a alegação de que é máximo quando.
Passo 1
a) Então pessoal, para descobrirmos quando é máximo, teremos que utilizar os conceitos de máximos e mínimos, ok? Sendo assim, temos que derivar a equação de e igualar a zero em seguida, saca só:
A solução para esse produto é a seguinte:
Como não está no domínio, temos que, de fato, é o ponto para que seja máximo.
Passo 2
b) Substituindo os pontos cedidos pelo enunciado, teremos uma equação dessa forma:
Plotando o gráfico, teremos:
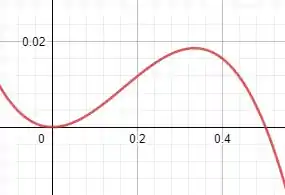
Pelo gráfico notamos que, de fato, é o ponto para que é máximo. Para , resulta em , exatamente o máximo absoluto dentro do intervalo em questão!
Resposta
Ei, a resposta está no passo a passo :)