Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.Exercícios Práticos - Ex. 29

Esboce uma parte do campo de direções da equação. Em seguida, adicione ao seu desenho a curva integral que passa pelo ponto P = ( 1 , - 1 ) . Use o método de Euler com x 0 = 1 e d x = 0,2 para estimar y ( 2 ) . Arredonde suas respostas até a quarta casa decimal. Determine o valor exato de y ( 2 ) para comparação.

y ' = x

Passo 1

Bom, primeiramente, se y ' = x então a gente tem que resolver a equação diferencial para encontrar y .

Vamos lá...

y ' = x → d y d x = x → d y = x d x

Integrando os dois lados, ficamos com:

y = x 2 2 + C

A gente faz o campo de direção dessa função então.

Passo 2

Para achar a curva integral que passa por P ( 1 , - 1 ) é só substituir e achar a constante...

y = x 2 2 + C

- 1 = 1 2 + C

C = - 3 2

Então, a curva integral que queremos é y = x 2 2 - 3 2

Passo 3

Vamos aplicar o método de Euler agora para obter o valor aproximado de y ( 2 ) .

O valor exato de y 2 = 2 2 2 - 3 2 = 2 - 3 2 = 1 2 = 0,5 então, o valor exato é 0,5 , e o valor aproximado é 0,4 .

Passo 4

O esboço do campo de direção e da curva integral pedida é:

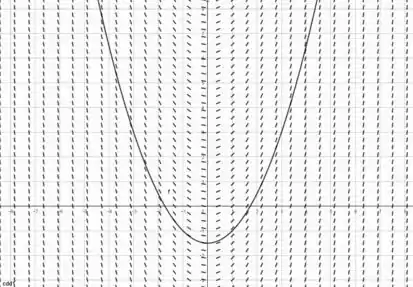
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aproximação do equilíbrio por duas trajetórias. Mostre que as duas trajetórias que conduzem a ( m / n ,a / b ) mostradas na Figura 9.31 são únicas por meio dos passos seguintes.A partir do sistema 1 a
Difusão de informação. Os sociólogos reconhecem um fenômeno chamado difusão social, que é a propagação de uma informação, inovação tecnológica ou modismo cultural entre a população. Os membros da popu
As equações diferenciais autônomas representam modelos de crescimento populacional. Use a análise da reta de fase para esboçar curvas integrais P ( t ) , selecionando diferentes valores iniciais P ( 0
Variação catastrófica no crescimento logístico. Suponha que uma população saudável de algumas espécies cresça em um ambiente limitado e que a população atual P 0 esteja bastante próxima da capacidade
Corrente em um circuito RL. O diagrama a seguir representa um circuito elétrico cuja resistência total é uma constante R ohms e cuja autoindutância, mostrada como uma espiral, é L henries, também cons