Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.4 - Ex. 71

71. Fórmula da área para parábolas de Arquimedes Arquimedes (287- 212 a.C.), inventor, engenheiro militar, médico e o maior matemático da época clássica no mundo ocidental,

descobriu que a área sob um arco parabólico é dois terços da base vezes a altura. Esboce o arco parabólico y = h - 4 h b 2 x 2 ,     - b / 2 < x < b / 2 , supondo que h e b sejam positivos. Em seguida, use o cálculo para determinar a área da região compreendida entre o arco e o eixo x.

Passo 1

Vamos esboçar o gráfico de

y = h - 4 h b 2 x 2 ,     - b 2 < x < b 2

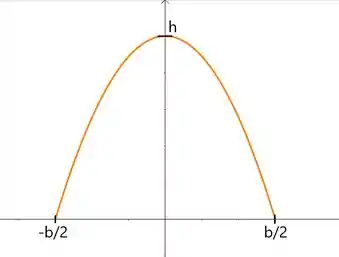
Essa é uma função de segundo grau, como o coeficiente do x 2 é negativo, a parábola tem a concavidade para baixo.

Quando x = 0 :

y = h - 4 h b 2 0 2

y = h

Ou seja a parábola cruza o eixo y em y = h

Quando y = 0 :

0 = h - 4 h b 2 x 2

h = 4 h b 2 x 2

x 2 = b 2 4

x = ± b 2 4

x = ± b 2

Então a parábola cruzo o eixo x em x = ± b / 2 :

O gráfico vai ficar dessa forma:

Passo 2

Vamos usar o cálculo para determinar a área sob a curva.

Se integrarmos a função y de - b / 2 até b / 2 vamos obter a área que queremos:

A = ∫ - b / 2   b / 2   h - 4 h b 2 x 2 d x

A = h x - 4 h b 2 x 3 3 - b 2 b 2  

A = h b 2 - 4 h b 2 ⋅ b 2 3 3 - h - b 2 - 4 h b 2 ⋅ - b 2 3 3  

A = h b 2 - h b 6 - - h b 2 + h b 6

A = h b 2 - h b 6 + h b 2 - h b 6

A = h b - h b 3

A = 2 h b 3

Resposta

A = 2 h b 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função. y = ∫ 1 cos ⁡ x 1 + v 2 10 d v
Use a parte 1 do Teorema fundamental do Cálculo para encontrar a derivada da função. G x = ∫ x 1 cos ⁡ t d t
68-a) Em qual intervalo aberto a fórmula F x = ∫ 1 x 1 t 2 - 9 d t representa uma antiderivada de f x = 1 x 2 - 9? b)Encontre um ponto em que o gráfico de F cruza o eixo x .
54. Explique por que o Teorema Fundamental do Cálculo pode ser aplicado sem modificações a integrais definidas em que o limite de integração inferior é maior do que ou igual ao limite de integração su
Use a geração de gráficos e a integração numérica de um CAS para gerar o gráfico da função F do Exercício 65 no intervalo - 20≤x≤20 e confirme que o gráfico está de acordo com os resultados obtidos na