Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.6 - Ex. 66

Use a geração de gráficos e a integração numérica de um CAS para gerar o gráfico da função do Exercício 65 no intervalo e confirme que o gráfico está de acordo com os resultados obtidos naquele exercício.

Passo 1

Vamos relembrar que função é essa e o os resultados desse exercício.

E no exercício, achamos que:

- o mínimo de está em

- é crescente em e decrescente em

- é côncava para cima em e para baixo em e

Precisamos confirmar essas afirmações aí, olhando o gráfico de . Vamos lá!

Passo 2

Vamos usar o Wolfram Mathematica para esboçar o gráfico de . Fica assim:

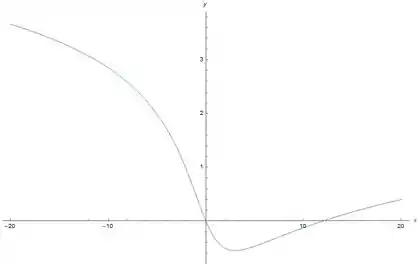
Por esse gráfico a gente confirma que todas as afirmativas estão certas. O mínimo está em , logo, antes desse ponto a função decresce e depois cresce.

E a nossa função muda de concavida em e .

Muito bonita a matemática. haha

Resposta

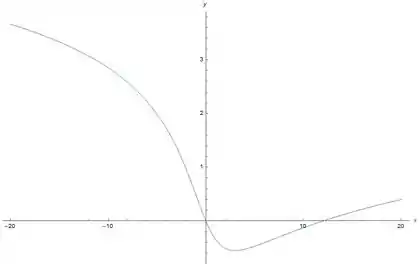
Os resultados obtidos no exercício 65 estão corretos.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a parte 1 do Teorema fundamental do Calculo para encontrar a derivada da função y = ∫ 1 cos ⁡ x 1 + v 2 10 d v

67-a) Em qual intervalo aberto a fórmula F x = ∫ 1 x d t t representa uma antiderivada de f x = 1 x? b)Encontre um ponto em que o gráfico de F cruza o eixo x .

68-a) Em qual intervalo aberto a fórmula F x = ∫ 1 x 1 t 2 - 9 d t representa uma antiderivada de f x = 1 x 2 - 9? b)Encontre um ponto em que o gráfico de F cruza o eixo x .

54. Explique por que o Teorema Fundamental do Cálculo pode ser aplicado sem modificações a integrais definidas em que o limite de integração inferior é maior do que ou igual ao limite de integração su