Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 11
7-18 Esboce a região englobada pelas curvas e encontra a área
11. , , ,
Passo 1
Vamos começar falando a fórmula que vamos usar nessa questão:
Essa fórmula é a 6.1.4 Fórmula para a área trocando por
Se e forem contínuas e em cada de , então a área da região limitada à esquerda por , à direita por , acima por e abaixo pela reta.
Podemos desenhar o gráfico e assim descobrir as propriedades que limitam essa curva!
Esse gráfico seria um pouco complicado, irei fazer apenas percebendo algumas coisas, mas no final boterei um gráfico para você perceber que estava certo!
Passo 2
Vamos começar com as limitações que são as suas limitações por cima e por baixo!
Quem limita essa curva por cima?
ou
Ora, é só você ver quem é o maior! O maior é o , então ele limita acima, então o da nossa fórmula é igual a e quem limita por baixo é o termo , então o . Pronto, já temos e .
Agora precisamos descobrir qual função é a da esquerda ou qual função é da direita! Uma ideia caso você não saiba desenhar o gráfico é que você pode escolher ao acaso e caso a área dê negativa, então a sua escolha foi equivocada!!!
No nosso problema, temos a reta e a curva , no intervalo de [o é positivo, então também é, então temos que o gráfico está todo a direita da reta !!
Podemos afirmar então que a curva delimita à direita e delimita à esquerda, portanto:
Montando a nossa integral, temos:
Passo 3
Paramos na expressão da integral, então voltaremos dela!
Vamos fazer primeiro a integral indefinda!
Então fazendo e , sabendo que .
Voltando para a integral definida:
Então a área é:
Se fôssemos desenhar o gráfico, teríamos:
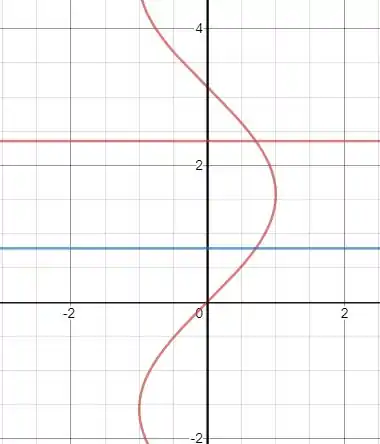
A reta em vermelho é e em azul !
Como previsto pela gente! Delimitação à esquerda é dada por à direita é dada por . Por baixo é delimitada por e por cima .