Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.9 - Ex. 45

Ache a área da região limitada pela curva y = s e n   x ,   pela reta y = 1 e pelo eixo y à direita do eixo y.

Passo 1

Observando o gráfico de cada curva, teremos:

Curva 1 – y = s e n   x → f 1 x = s e n   x   :

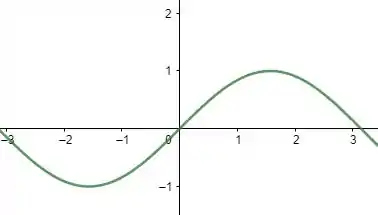
Curva 2 - y = 1 → f 2 x = 1 :

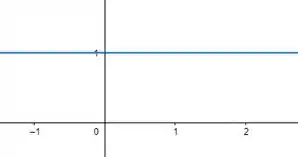
Curva 3 – x = 0 :

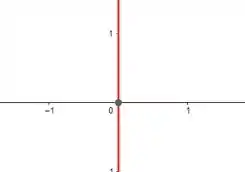
Passo 2

Calculando os pontos de interseção:

Curva 1 e 2:

s e n   x = 1 → x = 2 k π + π 2 → x = 4 k + 1 π 2   e   y = 1 → C = π 2 , 1

Curva 1 e 3:

y = s e n   0 = 0 → A = ( 0,0 )

Curva 2 e 3:

x = 0   e   y = 1 → B = 0,1

Passo 3

Juntando os gráficos, teremos:

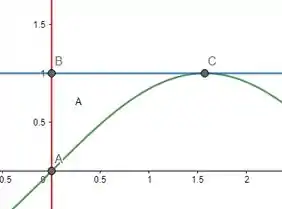
Dessa maneira, calcularemos a área como:

A = ∫ f x d x ,   o n d e   f x = f 2 x - f 1 x → f x = 1 - s e n   x

A = ∫ 0 π 2 1 - s e n x d x → [ x + cos ⁡ x ]   π 2 0 = π 2 + cos ⁡ π 2 - 0 - cos ⁡ 0 → A = π 2 - 1   u . a .

Resposta

Dessa maneira, a área será A = π 2 - 1   u . a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7-18 Esboce a região englobada pelas curvas e encontra a área12. x 2 = y , x = y - 2
7-18 Esboce a região englobada pelas curvas e encontra a área17. y = 2 + x - 1 , y = - 1 5 x + 7
7-18 Esboce a região englobada pelas curvas e encontra a área8. y = x 3 - 4 x , y = 0 , x = 0 , x = 2
7-18 Esboce a região englobada pelas curvas e encontra a área15. y = 2 x 2 + 1 , y = x
19-26.Use um recurso gráfico computacional, quando necessário, para encontra a região englobada pelas curvas.20. y = x 3 - 2 x 2 ,y = 2 x 2 - 3 x