Ache, por integração, a área do trapézio tendo vértices:
Passo 1
Colocando os pontos no gráfico, teremos:
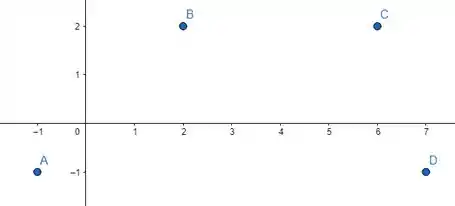
Passo 2
Daí, dividiremos o trapézio em 4 funções:
- é reta entre os pontos , logo:
- é reta entre os pontos , logo:
- é reta entre os pontos , logo:
- é reta entre os pontos , logo:
Passo 3
Calculando as áreas, teremos que dividir o trapézio em três:
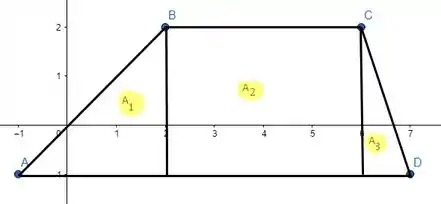
- Área entre :
- Área entre :
- Área entre :
Resposta
Dessa forma,