Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.Revisão - Ex. 83
83)S eja f a função definida por
- Faça um esboço do gráfico de
- Para quais valores de a existe
- Em quais números é contínua?
Passo 1
O exercício solicita na letra a) que se faça um esboço do gráfico.
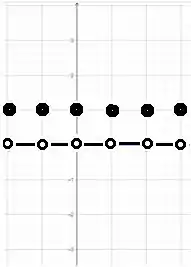
Passo 2
A alternativa b) soliticita para quais valores existe o limite da função quando x tender a “a”. Para isso precisamos avaliar 2 casos; quando “a” for inteiro e quando “a” não for inteiro.
Se “a” inteiro, e para todo x nos intervalos
Portanto:
Se “a” não é inteiro, e está no intervalo para algum inteiro k. Então para todo x no intervalo
Portanto:
Então conclui-se que o existe para todo a.
Passo 3
A letra c) do exercício pergunta em quais números a função é contínua. Pelo gráfico observa-se que ela será contínua em todos os valores reais exceto nos números inteiros.
Resposta
a)
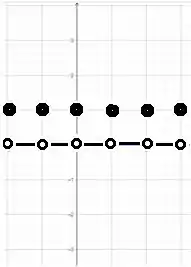
b) O existe para todo a.
c) f é contínua para todos os números reais exceto números inteiros.