Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.Revisão - Ex. 86
86) Trace um esboço do gráfico de g se
a) O existe?
b) é contínua em 1?
Passo 1
O exercício solicita inicialmente que se faça um esboço do gráfico no intervalo . Trata-se da função menor inteiro. Iremos atribuir alguns valores para x para facilitar a visualização do comportamento dessa função no intervalo desejado.
Para qualquer valor no intervalo teremos a função constante ; e no intervalo teremos a função do 1º grau ;
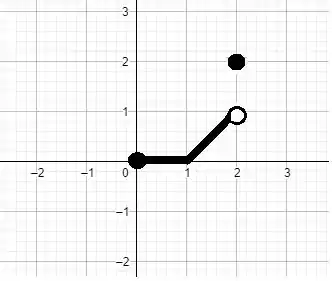
Passo 2
A alternativa b) pergunta se existe o limite de quando x tender a zero. Para verificar isso calculamos os limites laterais da função tendendo a zero pela direita e pela esquerda
Portanto verifica-se que existe.
Passo 3
A letra c) do exercício pergunta se a função é contínua em 0. Para isso é preciso verificar se
Como e a função é contínua em
Resposta
Gráfico:
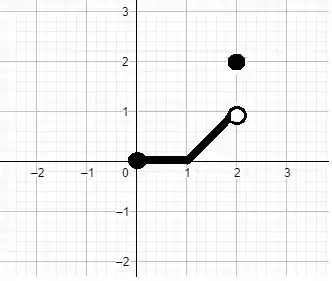
a) Existe.
b) É contínua.