Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.Revisão - Ex. 84

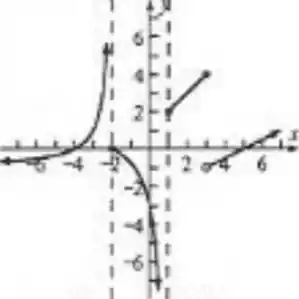
84) Faça um esboço do gráfico de uma função f que satisfaça as seguintes condições : f é contínua em - ∞ , - 2 , - 2,1 , 1,3 e   3 , + ∞ ;   lim x → - 4 ⁡ f x = 0 ; lim x → - 2 ⁡ f x = + ∞ ;   lim x → - 2 + ⁡ f x = 0 ;   lim x → 0 ⁡ f x = - 3 ;   lim x → 1 - ⁡ f x = - ∞ ;   lim x → 1 + ⁡ f x = 2 ;   lim x → 3 - ⁡ f x = 4 ;   lim x → 3 + ⁡ f x = - 1 ; lim x → 5 ⁡ f x = 0   .

Passo 1

Vamos analisar a influência de cada um dos limites fornecidos no enunciado para a construção do gráfico da função.

  1. Como: lim x → - 4 ⁡ f ( x ) = 0 e f é contínua em - 4 , f ( - 4 ) = 0 , ou seja o gráfico contém ( - 4,0 ) .

  2. lim x → - 2 - ⁡ f ( x ) = + ∞ , logo assíntota vertical em x = - 2 .

  3. Como: lim x → - 2 + ⁡ f ( x ) = 0 , f ( 2 ) = 0 . Ou seja, o gráfico contém o ponto ( - 2,0 ) .

  4. lim x → 0 ⁡ f ( x ) = - 3 e f é contínua, então f ( 0 ) = - 3 , ou seja o gráfico contém o ponto ( 0 , - 3 ) .

  5. lim x → 1 - ⁡ f ( x ) = - ∞ , logo assíntota vertical em x = 1 .

  6. Como: lim x → 3 - ⁡ f ( x ) = 4 e f é contínua a esquerda de 3, o gráfico contém o ponto 3,4 .

  7. Como: lim x → + ⁡ f x = - 1 o ponto ( 3 , - 1 ) é “bolinha aberta”

  8. lim x → 5 ⁡ f x = 0 , logo o gráfico contém o ponto ( 5,0 ) .

Colocando todas essas informações no gráfico obtemos o seguinte esboço:

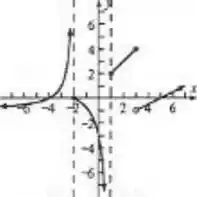
Resposta

Gráfico:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os exercícios de 99 e 100 referem-se à Secção Suplementar 2.10. 100) Dada f x = x - 2 x + 5 .(a) Determine os valores de k tais que lim x → k ⁡ f x0 , (b) Ache todos os intervalos abertos (a,b) conten
85) Trace um esboço do gráfico de f se f x = 1 - x 2e- 2 ≤ x ≤ 2 . ⟦ ⟧ a) O lim x → 0 ⁡ f x existe?b )f é contínua em 0?
92) Dê exemplo de uma função f que seja descontínua em 1, para qual (a) lim x → 1 ⁡ f x existe, mas f ( 1 ) não existe;(b) f ( 1 ) existe, mas lim x → 1 ⁡ f x não existe;(c) f ( 1 ) e lim x → 1 ⁡ f x
91)(a) Prove que se lim h → 0 ⁡ f x + h = f x , então lim h → 0 ⁡ f x + h = lim h → 0 ⁡ f x - h (b) Mostre que o inverso do teorema (2) não é verdadeiro, dando exemplo de uma função para a qual lim h
93) Se o domínio de f for o conjunto de todos os números reais e se f for contínua em 0, prove que se f a + b = f a + f b para todo a e b, então f será contínua em todo número.