Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.2 - Ex. 28

25-32 Use a derivada dada para encontrar todos os pontos críticos de f e, em cada um deles, determine se ocorre um máximo relativo, um mínimo relativo ou nenhum desses. Suponha, em cada caso, que f seja contínua em toda parte.

28. f ' x =   x 2 - 7 x 2 + 4 3

Passo 1

Galera, vamos começar lembrando quais são as condições necessárias para x 0 ser ponto crítico da nossa função:

- f ' x 0 = 0

-   f não é diferenciável em x 0 .

Perceba que o denominador da nossa função racional nunca se anula, pois a parte de dentro é a parábola   x 2 com concavidade para cima deslocada quatro unidades para cima sobre o eixo y. Ou seja, ela não intercepta o eixo x em nenhum ponto. Além disso, é sempre positiva.

Assim, a nossa f é diferenciável para todo x .

Passo 2

Agora, o que nos resta é igualar a nossa função a zero. Assim, vamos ter

x 2 - 7 x 2 + 4 3 = 0

x 2 = 7

x = ± 7

Passo 3

Nós já achamos os nossos pontos críticos. O próximo passo é aplicar o teste da primeira derivada. Para isso, a gente vai precisar estudar o sinal da nossa função antes e depois dos nossos pontos críticos. Eu acho que isso vai ficar mais fácil com o auxílio de uma tabela. Então, bora lá.

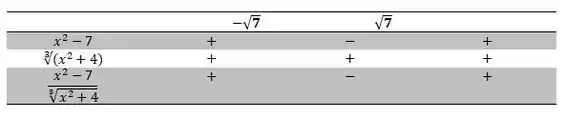
Passo 4

Agora que já montamos a nossa tabela, é só analisar os dados obtidos. Então, vem comigo!!!

Como à esquerda de   - 7   é positivo e à direita é negativo,   - 7   é máximo relativo. Já no caso do   7   , à sua esquerda é negativo e à sua direita é positivo. Portanto, é mínimo relativo.

Resposta

- 7   : máximo relativo;

7   : mínimo relativo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .d) A função f tem exatamente dois extremos relativos no intervalo I e f x → - ∞ quando x → +
2. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .a) f tem exatamente um extremo relativo em I e f x → 0 quando x → + ∞ e x → - ∞ .
1. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .b) f é côncava para cima no intervalo I e não tem extremos relativos.
3. a) Use os testes da derivada primeira e da derivada segunda para mostrar que f x = 3 x 2 - 6 x + 1 tem um mínimo relativo em x = 1 .
6. a) Mostre que f x = 1 - x 5 e g x = 3 x 4 - 8 x 3 têm pontos estacionários em x = 0 .b) O que o teste da derivada segunda diz sobre a natureza desses pontos estacionários?c) O que o teste da deriva