Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.6 - Ex. 42

Ache, com aproximação de 1 grau, as medidas dos ângulos internos do triângulo com vértices (1, 0), (-3, 2) e (2, 3).

Passo 1

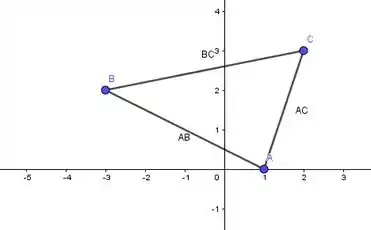
Vamos definir: A(1, 0), B(-3, 2) e C(2, 3).Inicialmente vamos marcar os pontos no plano cartesiano e fazer o esboço do triângulo. Assim:

Passo 2

Vamos determinar a inclinação de cada lado do triângulo.

→ L a d o   A B :

m A B = 2 - 0 - 3 - 1 ⇒

m A B = 2 - 4 ⇒

m A B = - 1 2

→ L a d o   A C :

m A C = 3 - 0 2 - 1 ⇒

m A C = 3 1 ⇒

m A C = 3

→ L a d o   B C :

m B C = 3 - 2 2 - ( - 3 ) ⇒

m B C = 1 2 + 3 ⇒

m B C = 1 5

Passo 3

Vamos determinar o ângulo entre cada par de lado do triângulo.

→ E n t r e   A B   e   A C :

t g θ 1 = - 1 2 - 3 1 + - 1 2 . ( 3 ) ⇒

t g θ 1 = - 1 - 6 2 1 - 3 2 ⇒

t g θ 1 = - 7 2 - 1 2 ⇒

t g θ 1 = 7 ⇒

θ 1 = a r c t g ( 7 ) ⇒

θ 1 = 82 ◦

→ E n t r e   A C   e   B C :

t g θ 2 = 3 - 1 5 1 + 1 5 . ( 3 ) ⇒

t g θ 2 = 15 - 1 5 1 + 3 5 ⇒

t g θ 2 = 14 5 8 5 ⇒

t g θ 2 = 14 5 . 5 8 ⇒

t g θ 2 = 14 8 ⇒

θ 2 = a r c t g 14 8 ⇒

θ 2 = 60 ◦

→ E n t r e   A B   e   B C :

t g θ 3 = - 1 2 - 1 5 1 + - 1 2 . 1 5 ⇒

t g θ 3 = - 5 - 2 10 1 - 1 10

t g θ 3 = - 7 10 9 10 ⇒

t g θ 3 = - 7 10 . 10 9 ⇒

t g θ 3 = - 7 9 ⇒

θ 3 = a r c t g - 7 9 ⇒

θ 3 = 38 ◦

Resposta

Portanto, os ângulos internos do triângulo com vértices (1, 0), (-3, 2) e (2, 3) são 82◦, 60◦ e 38◦.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça os gráficos das funções nos Exercícios 23-26 no plano t s (eixo t horizontal, eixo s vertical). Qual é o período de cada função? Que simetrias os gráficos possuem?23. s = c o t g2 t
28. Faça um gráfico y = tg ⁡ x e y = co tg ⁡ x juntos para - 7 ≤ x ≤ 7 . Comente o comportamento de co tg ⁡ x em relação aos sinais e valores de t g ⁡ ( x )
No exercício a seguir é dado um dos valores de s e nx , cos ⁡ x e t gx . Determine os outros dois valores quando x está no intervalo especificado. cos ⁡ x = 1 3 ,x ∈- π 2 , 0
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função? c o s( π x 2 )
No exercício a seguir é dado um dos valores de s e nx , cos ⁡ x e t gx . Determine os outros dois valores quando x está no intervalo especificado. t gx = 1 2 ,x ∈ [π , π 2]