Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 42

Ache a área de uma folha da rosácea r = 2 s e n 3 theta .

Passo 1

Para entender melhor a questão é bom ter uma ideia de como é o gráfico da rosácea.

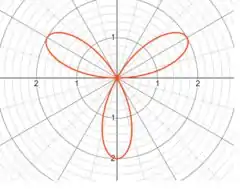
A área que a questão pede é somente de uma folha.

Passo 2

Desse modo, fica a critério do leitor qual das regiões escolher para solucionar a questão. Para efeitos didáticos optou-se a folha compreendida entre os ângulos 0 e (pi)/(2) .

Passo 3

Portando, e sabendo que a área da região é dada por:

A = (1)/(2) int_(alpha)^(beta) [f (theta)]^2 d theta = (1)/(2) int_0^((pi)/(2)) 4 s e n^2 3 theta d theta .

Para resolver esta integral, basta lembra da propriedade trigonométrica. Portanto,

A = (1)/(2) int_0^((pi)/(2)) 4 * (1)/(2) * [1 - cos (2 * 3 theta)] d theta = int_0^((pi)/(2)) (1 - c o s 6 theta) d theta

A = [theta - (s e n 6 theta)/(6)] | 0(pi)/(2) = (pi)/(2)

Resposta

A = (pi)/(2) u.a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 33 a 3 7 , encontrar o comprimento de arco da curva dada.
Nos exercícios 9 a 32 esboçar o gráfico das curvas dadas em coordenadas polares.
Nos exercícios 9 a 32 esboçar o gráfico das curvas dadas em coordenadas polares.
Nos exercícios 9 a 32 esboçar o gráfico das curvas dadas em coordenadas polares.
Nos exercícios 9 a 32 esboçar o gráfico das curvas dadas em coordenadas polares.