Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 43

Ache a área da região interior ao gráfico de r = 2 a   s e n θ e exterior ao gráfico de r = a .

Passo 1

Para entender melhor a questão é bom ter uma ideia de como as funções comportam-se no gráfico.

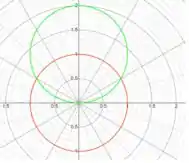
A área que a questão pede está dento do círculo verde e fora do círculo vermelho.

Passo 2

Desse modo, se faz necessário saber os ângulos de intersecção, para isso, basta igualar as duas equações. Com isso,

2 a   s e n θ = a

s e n θ = 1 2

Lembre-se que há dois ângulos no círculo trigonométrico em que o seno é igual a um meio.

Logo, θ 1 = π 6 e θ 2 = 5 π 6 .

Passo 3

Portanto, e sabendo que a área da região é dada por:

A = 1 2   ∫ α β f θ 2 - g θ 2 d θ

Aplicando, temos:

A = 1 2 ∫ π 6 5 π 6 4 a 2 s e n 2 θ - a 2 d θ

Um dos meios de resolver essa integração é aplicando uma propriedade trigonométrica, assim:

A = 1 2 ∫ π 6 5 π 6 4 a 2 * 1 2 ( 1 - c o s 2 θ )   - a 2 d θ

A = 1 2 2 a 2 θ - a 2 s e n 2 θ - a 2 θ |   π 6 5 π 6

A = 1.91 a 2

Resposta

1.91a²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 39 a 46 , encontrar a integral que dá o comprimento total da curva dada.
Nos exercícios de 39 a 46 , encontrar a integral que dá o comprimento total da curva dada.
Nos exercícios de 39 a 46 , encontrar a integral que dá o comprimento total da curva dada.
Nos exercícios de 47 a 56 , calcular a área limitada pela curva dada.
Nos exercícios de 47 a 56 , calcular a área limitada pela curva dada.