Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 31
No exercício a seguir, ache a equação cartesiana do gráfico tendo a equação polar dada.
Passo 1
Legal, temos que transformar essa nossa amiga aí em uma equação cartesiana (do tipo mais comum com x e y). Primeira coisa que você tem que fazer é aquela nossa coisa que já tá batida e você deve ter na ponta da língua! As relações de r com x e y.
Passo 2
SIMBORA PRAS CONTINHAS! Então galera, essa questão precisa de todo nosso amor, carinho e atenção, tudo pra combinar com a essência dessa questão. Não entendeu? Aqui estamos tratando de uma ROSA POLAR! Sim, e vamos tratar essa flor com carinho e amor para conseguir resolver ela.
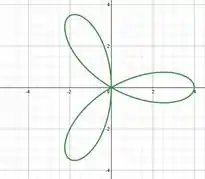
Tá ai o formato da nossa flor, linda, não?
Essas rosas polares tem uma regra pra serem seguidas:
No qual a significa o tamanho de uma pétala no eixo x e k obedece uma relação em que:
Seguindo essa “matriz” floral
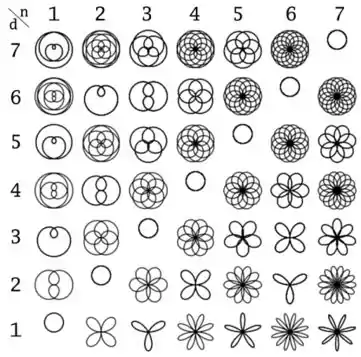
Incrível né? Mas vamo deixar de enrolação e partir pra conversão dessa equação polar em cartesiana!
Passo 3
Sabendo que essa rosácea segue a lei básica das leminiscatas de Bernoulli:
Logo,