Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.5 - Ex. 44

Ache a área da região limitada pela curva y = e x e pela reta que passa pelos pontos ( 0 ,   1 ) e ( 1 ,   e ) .

Passo 1

Antes de começar precisamos encontrar a reta que passa pelos pontos ( 0 ,   1 ) e ( 1 ,   e ) .

Sendo a estrutura de uma reta: y = a x + b , podemos encontrar a equação da reta substituindo x e y dos nossos pontos:

1 = a ⋅ 0 + b

e = a ⋅ 1 + b

b = 1

a = e - 1

Logo, nossa reta é dada por:

y = e - 1 x + 1

Agora vamos determinar as extremidades do nosso problema.

Para isso precisamos saber quem fica por cima, a reta ou a curva. O gráfico de y = e x já está ficando comum entre nós, ele é um gráfico exponencial que cresce para o + ∞ , logo ele tem uma concavidade para baixo, isso é explicado pela segunda derivada y ' ' = e x > 0 .

Já nossos pontos são justamente onde a curva e a reta se tocam. Se a concavidade é para baixo então vem a curva y = e x primeiro e em seguida a reta y = e - 1 x + 1 . Olha como seria no gráfico.

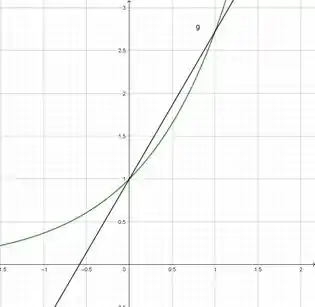
Logo nossa região está acima da curva y = e x , abaixo da reta y = e - 1 x + 1 no intervalo fechado 0 ,   1 .

Passo 2

Com essas informações podemos montar nossa integral, lembre-se que os intervalos são os limites da integral e dentro da integral colocamos a função de cima menos a de baixo.

∫ 0 1 e - 1 x + 1 - e x   d x

Agora podemos resolve-la e finalmente realizar a subtração com os limites da integral:

= e - 1 x 2 2 + x - e x 0 1

= e - 1 2 + 1 - e - 0 + 0 - e 0

= e - 1 2 + 1 - e + 1 = 3 - e 2

Resposta

= 3 - e 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área das regiões delimitadas pelas curvas e retas y 2 = 4 x , y = 4 x - 2
Determine a área da região cortada do primeiro quadrante pela curva x 1 2 + y 1 2 = a 1 2
Determine a área entre a curva y = 1 x e o eixo x de x = 10 até x = 20 é a mesma área entre a curva e o eixo x de x = 1 até x = 2 .
Determine a área total da região delimitada pela curva = s e n x , y = c o s x0 ≤ x ≤ 3 π 2
Determine a área entre a curva y = 1 x e o eixo x de k a até k b é a mesma área entre a curva e o eixo x de x = a até x = b . ( 0ab , k0 ).