Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.2 - Ex. 39
Ache a área da região limitada pela curva e pelo eixo de e .
Passo 1
Primeiro passo é identificar que área é essa, né? Mas desenhar o gráfico da função dada não é tão intuitivo, na verdade, nem precisamos, pois essa é uma função positiva, pessoal. Nesse caso, ao calcular a integral em certo intervalo, o resultado é justamente a área!
Mas qual seria o nosso intervalo? O problema disse que a área é limitada pela curva, eixo de a , então o intervalo de integração é .
Vamos ver o gráfico da função só para confirmar os dados:
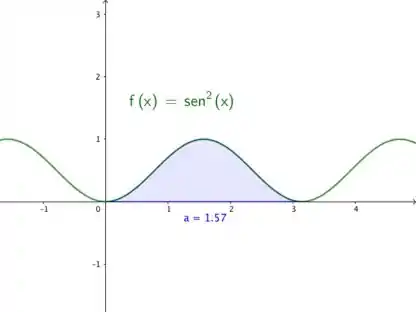
Passo 2
A área de acordo com os dados anteriores é dada pela integral:
Antes de resolver, precisamos usar uma relação trigonométrica para virar uma integral imediata. A relação é:
Ficamos então com:
Passo 3
Para resolver essa última integral, vamos usar:
Daí temos:
Sabemos da integral definida que:
Em que é uma primitiva de . Diante disso,
Logo, a área é:
significa é unidades de área.