Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.2 - Ex. 20
Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.
Focos em e e a constante mencionada na definição 10.2.1 é .
Passo 1
A questão pede para acharmos a equação da elipse com focos e . Além disso, é dito que a constante é igual a . Assim, já temos que .
Agora só precisamos do centro da elipse e de . Note que os focos estão sobre o eixo , de modo que o eixo maior da elipse está sobre esse eixo. O centro será o ponto médio dos focos:
Assim, o centro será a origem . Vemos assim que a distância de um dos focos até o centro é .
Passo 2
Já temos que e . Assim,
Portanto, a equação da elipse será:
Passo 3
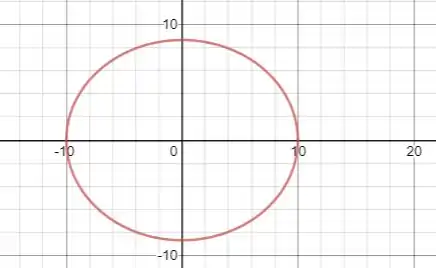
O esboço da elipse é mostrado a seguir:
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas 28 a 33, determinar a equação reduzida, o centro, os vértices A 1 e A 2 , os focos e a excentricidade das elipses dadas. Esboçar o gráfico 16 x 2 + y 2 + 64 x - 4 y + 52 = 0
Em cada um dos problemas 28 a 33, determinar a equação reduzida, o centro, os vértices A 1 e A 2 , os focos e a excentricidade das elipses dadas. Esboçar o gráfico 25 x 2 + 16 y 2 + 50 x + 64 y - 311
Em cada um dos problemas 28 a 33, determinar a equação reduzida, o centro, os vértices A 1 e A 2 , os focos e a excentricidade das elipses dadas. Esboçar o gráfico 4 x 2 + 9 y 2 - 24 x + 18 y + 9 = 0
Nos problemas 34 a 39, obter equações paramétricas da elipse de equação dada. x 2 + 4 y 2 = 4
Nos problemas 34 a 39, obter equações paramétricas da elipse de equação dada. x 2 + y 2 = 36