Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Elipse - Ex. 29
Em cada um dos problemas 28 a 33, determinar a equação reduzida, o centro, os vértices e , os focos e a excentricidade das elipses dadas. Esboçar o gráfico
Passo 1
Vamos começar achando a equação reduzida, juntando os e os
Show agora podemos visualizar melhor a sacada que vamos precisar!
O que vamos fazer agora é completar quadrados, lembrando que:
Então vamos acrescentar esse 2 e o 4 dentro dos parênteses, mas quando fazemos isso temos que compensar do outro lado, então vamos ter que acrescentar 25 e , no total temos que acrescentar 89do outro lado da equação, então ficamos com
Como a nossa equação tem que ser do tipo
Vamos dividir os dois lados por
Podemos ver então que nossa equação é da forma:
E o eixo maior ta em , ou seja nossa elipse é “em pé”
Então, podemos ver que
E nossa equação reduzida fica:
Passo 2
Com e podemos encontrar quem é nossa distancia focal , fazendo
Passo 3
Para acharmos os vértices, basta somar na coordenada e
Passo 4
Achando , podemos achar o foco, que vai ser no eixo , já que o eixo maior é nele, somando a coordenada do centro com , para achar os dois focos, ou seja,
Passo 5
Agora para achar a excentricidade é só lembrar da formulinha
Passo 6
Juntando esses resultados que achamos podemos desenhar a nossa elipse, que fica assim:
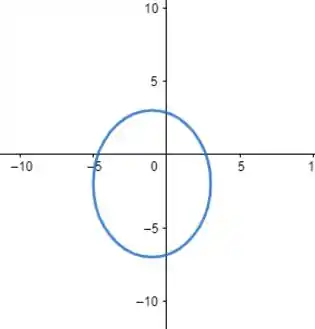
Resposta
Ei, a resposta está no passo a passo :)