Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 55
Ache a equação polar da cônica que satisfaz as condições dadas e faça um esboço gráfico. Um foco na origem; vétices em (2,) e (4,).
Passo 1
Note que, se colocarmos esses pontos no gráfico a figura mais provável seja uma hipebole. Desse modo, a equação geral para hipérbole é:
Passo 2
Sabendo disso, aplica-se os vértices dado na equação geral. Observer também, que o ponto (4,) pode ser também represetando por (-4,0). Portanto,
Isolando da primeira equação e aplicando na outra, temos
Assim,
Aplicando na primeira equação, temos
Passo 3
Logo, a equação da cônica é:
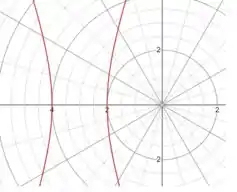
E o esboço gráfico é:
Resposta
Exercícios de Livros Relacionados
Assinalar o ponto dado em coordenadas polares e depois escrever as coordenadas polares para o mesmo ponto, tal que: r tenha sinal contrário θ tenha sinal contrário 2 , - π 3
Encontrar as coordenadas cartesianas do seguinte ponto dado em coordenadas polares. - 10 , π 2
Esboçar o gráfico da curva dada em coordenadas polares: r = 2cos 3 θ
Esboçar o gráfico da curva dada em coordenadas polares: r = 1 + 2 cos θ
Transformar a seguinte equação para coordenadas cartesianas. r = a ,a0