Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.Revisão - Ex. 42
Ache a equação da reta tangente à curva y = em (2,2)
Passo 1
Propriedades de Derivada
Sendo “a” uma constante.
Propriedade do Expoente
Passo 2
Primeiramente
Achar a reta tangente em uma curva num ponto é achar a derivada da função nesse ponto.
Queremos uma função neste formato : y = Ax +b
E sabemos que A =
Entao precisamos agora Derivar f(x)
=
No ponto onde x=2 temos :
=
= 2(ln2 +1/2 )
= 2 ln2 +1
Passo 3
Achando a equação da reta
y = Ax +b
Nosso ponto é (2,2)
Logo podemos achar b
2 =
B = -4 ln 2
A reta tangente é portanto y =
Olhando para o gráfico, temos em verde a curva f(x) e em azul a reta tangente elas se interceptando em (2,2)
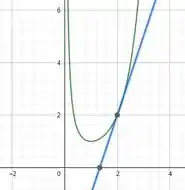
Resposta
A reta tangente é y =
Exercícios de Livros Relacionados
A função s t descreve a posição de uma partícula movendo-se ao longo de um eixo coordenado, onde s está em metros e t está em segundos.Encontre as funções velocidade e aceleração.Encontre no instante
É dada uma função posição de uma partícula que se move ao longo de uma reta coordenada.Estime s e v quando a = 0 .Estime s e a quando v = 0 . s = ln 3 t 2 - 12 t + 13
A função s t descreve a posição de uma partícula movendo-se ao longo de um eixo coordenado, onde s está em metros e t está em segundos.Encontre as funções velocidade e aceleração.Encontre no instante
É dada uma função posição de uma partícula movendo-se ao longo de um eixo coordenado. Use o método do Exemplo 6 para analisar o movimento da partícula em t ≥ 0 e faça um esboço esquemático do moviment
É dada uma função posição de uma partícula movendo-se ao longo de um eixo coordenado. Use o método do Exemplo 6 para analisar o movimento da partícula em t ≥ 0 e faça um esboço esquemático do moviment