Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.6 - Ex. 23
Ache os extermos relativos da função dada usando o teste da derivada segunda, uando aplicável. Quando ele não for aplicável, use o teste da derivada primeira.
Use a derivada segunda para encontrar os pontos de inflexão do gráfico da função e determine onde o gráfico é côncavo para cima e onde é para baixo. Faça um esboço do gráfico.
Passo 1
Vamos começar achandos os pontos críticos da função. Porque eles são os candidatos a extremo. Para isso vamos pegar a derivada de . Para isso, vamos usar a regra da cadeia
Vamos fazer
e
Então a derivada vai ficar:
Os pontos crítos são aqueles que a derivada é ou não existe. A derivada não vai existir quando o denominador for
No intervalo, não temos nenhum valor para isso.
Agora vamos igualar a derivada a
Fazendo:
No invervalo temos
Passo 2
Agora, vamos tentar aplicar o teste da segunda derivada, que vai ser exatamente o que está aqui embaixo, mas só vale para os pontos críticos
Se ou não existir, não funciona o teste.
Aplicando a regra do quociente:
Organizando isso:
Temos que
Logo é um ponto de mínimo.
Passo 3
Vamos agora para a concavidade
Temos no numerador uma soma de números ao quadrado, então ele será sempre positivo.
O denominador depende de , mas no intervalo que ele deu esse valor sempre vai ser positivo. Então
Para qualquer valor de , não tendo ponto de inflexão e sendo sempre côncava para cima.
Passo 4
Vamos organizar as informações para o nosso gráfico:
Mínimo relativo:
Concava para cima:
O esboço vai ficar:
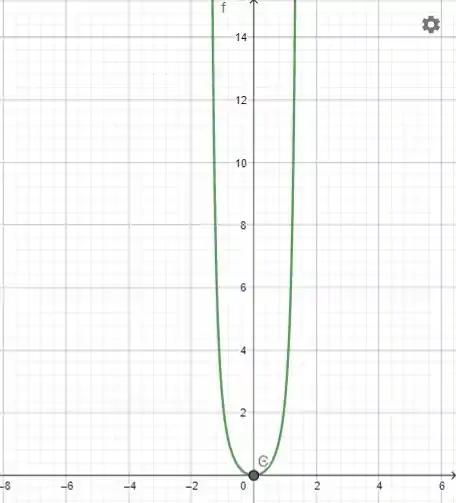
Resposta
Mínimo relativo:
Concava para cima:
O esboço vai ficar:
