Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.6 - Ex. 21
Ache os extermos relativos da função dada usando o teste da derivada segunda, uando aplicável. Quando ele não for aplicável, use o teste da derivada primeira.
Use a derivada segunda para encontrar os pontos de inflexão do gráfico da função e determine onde o gráfico é côncavo para cima e onde é para baixo. Faça um esboço do gráfico.
Passo 1
Vamos começar achandos os pontos críticos da função. Porque eles são os candidatos a extremo. Para isso vamos pegar a derivada de .
Os pontos crítos são aqueles que a derivada é ou não existe. Aqui só vamos olhar quando a derivada é .
Fazendo:
Passo 2
Agora, vamos tentar aplicar o teste da segunda derivada, que vai ser exatamente o que está aqui embaixo, mas só vale para os pontos críticos
Se ou não existir, não funciona o teste.
Vamos ter
Temos que ver o valor de para e
Primeiro :
Logo é ponto de Máximo relativo.
Passo 3
Agora :
Temos que ver se esse cara é positivo ou negativo. Para isso vamos racionalizar:
Assim:
Como é maior que , aquela subtração vai ser maior que . Então
Logo é ponto de máximo relativo.
Passo 4
Por fim
Agora :
Estamos com dois números negativos, então
Logo é ponto de mínimo relativo.
Passo 5
Vamos agora para a concavidade
Vamos analisar direto os sinais dessa função para achar a concavidade e de quebra os pontos de inflexão.
Para isso, vamos fazer:
Como temos apenas o , antes desse valor a função vai ser negativa e depois ela vai ser positiva.
Então, a função é côncava para baixo para valores menores que , e côncava para cima para valores maiores que .
Assim o ponto de inflexão é:
Passo 6
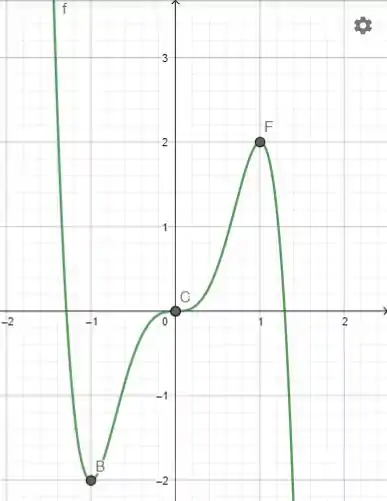
Vamos organizar as informações para o nosso gráfico:
Máximo relativo:
Mínimo relativo:
Ponto de inflexão:
Concava para cima:
Concava para baixo
O esboço vai ficar:
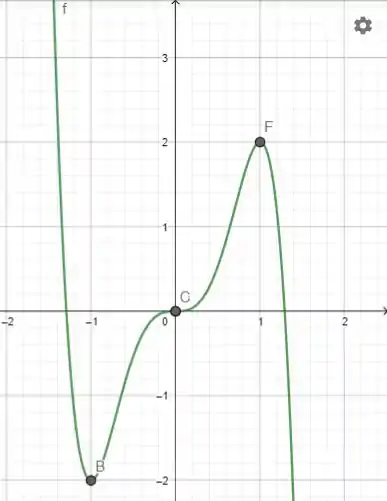
Resposta
Máximo relativo:
Mínimo relativo:
Ponto de inflexão:
Concava para cima:
Concava para baixo
O esboço vai ficar:
