Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 82
Ache a inclinação da reta tangente ao gráfico de r = no ponto (1,). Faça um esboço do gráfico com a reta tangente.
Passo 1
Primeiro, em questões que envolvem retas tangentes, sempre temos aquelas equaçõeszinhas que não podem se perderem na nossa mão!! Aí vão elas:
Logo, para o nosso caso, temos que:
Portanto:
Passo 2
Agora vamos resumir a nossa equação para então encontrarmos os pontos em que nossa retas são tangentes.
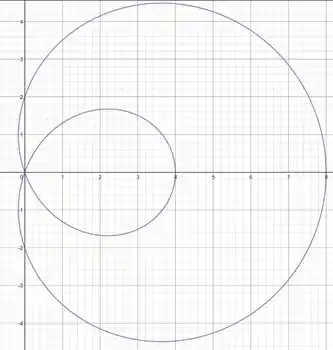
Para a nossa equação, temos esse esboço:
Passo 3
Resolvendo nossa equação para um theta igual a , temos que:
Resposta
Exercícios de Livros Relacionados
Mostre que x + y = a representa uma família monoparamétrica de de cônicas e determine o tipo da cônica. Faça um esboço do gráfico para a=1, a=2 e a=4.
Determine os pontos aos quais a curva r = 3 - 3 s e n ( θ ) tem retas tangentes horizontal e vertical. Faça um esboço gráfico com essas retas tangentes.
Determine os pontos aos quais a curva r = 3 - 3 s e n ( θ ) tem retas tangentes horizontal e vertical. Faça um esboço gráfico com essas retas tangentes.
Ache a inclinação da reta tangente ao gráfico de r = 1 2 + s e n θ no ponto (1, 1 6 π ). Faça um esboço do gráfico com a reta tangente.