Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 77
Mostre que representa uma família monoparamétrica de de cônicas e determine o tipo da cônica. Faça um esboço do gráfico para a=1, a=2 e a=4.
Passo 1
Beleza galera, essa equação nos parece um pouco estranha de cara né? Mas vamos por partes!
Ao pegarmos a equação e elevarmos ao quadrado, temos que:
E agora isolando o y, temos que:
Passo 2
Ora, isso é uma curva bem conhecida já não é ? ela representa uma curva no primeiro quadrante, que começa no eixo y em a e vai até o eixo x em a. Não entendeu? Vamos ao desenho!
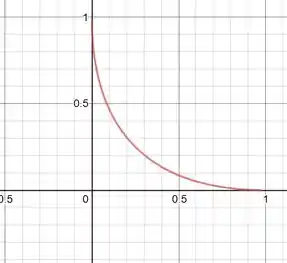
Essa é a curva do gráfico de a=1. Vamos para os esboços para os novos valores de “a”.
Passo 3
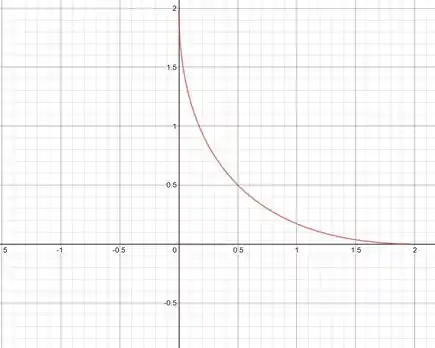
Esse é o gráfico para a=2.
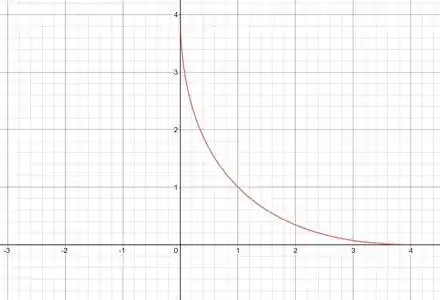
Esse é o gráfico para a=4.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Simplifique a equação dada por uma rotação e uma translação de eixos. Faça um esboço do gráfico e mostre os três conjuntos de eixos. 3 x 2 - 3 x y - y 2 - 6 y = 0
Simplifique a equação dada por uma rotação e uma translação de eixos. Faça um esboço do gráfico e mostre os três conjuntos de eixos. 4 x 2 + 3 x y + y 2 - 6 x + 12 y = 0
A órbita do planeta Mercúrio em torno do Sol é elíptica com o Sol em um foco, um semi-eixo maior com comprimento de 58 milhões de quilômetros e uma excentricidade de 0,206. Ache (a) a menor distância
Um satélite gira em torno da terra numa órbita elíptica com excentricidade 1/3 e tendo a terra em um foco. A menor distância do satélite à terra é de 300 Km. Ache a maior distância entre o satélite e
Encontre o volume do sólido gerado pelo giro da região delimitada pela elipse 9x2 + 4y2 = 36 em torno do (a) eixo x, (b) eixo y.