Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 84
Prove que os gráficos de r= e têm um numero ilimitado de pontos de intersecção. Pronve também que as retas tangentes a esses pontos são perpendiculares.
Passo 1
Podemos adotar o r dado como uma curva polar, logo, o nosso e são inversos, com isso podemos transformar essas curvas polares em curvas no domínio cartesiano. Com as nossas transformações básicas de cartesiano para polar e vice-versa.
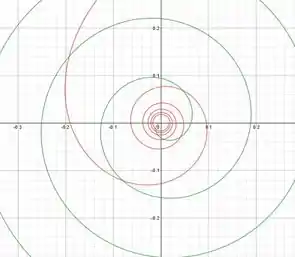
Passo 2
Temos então que nosso e que o nosso logo derivando nossos x e y, obtermos as retas tangentes das duas curvas polares.
Passo 3
Portanto, vamos ao esboço com a reta indicada:
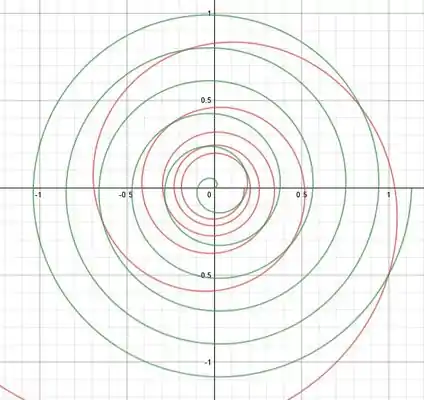
Estando assim, provado que ele toca em infinitos pontos.
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com