Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.9 - Ex. 51

Ache a taxa de variação da medida da área no Exercício 49 em relação a p e quando p=3.

Passo 1

Observando o gráfico de cada curva, teremos:

  • f 1 x = 4 p x   o u   f 2 x = - 4 p x :

  • f 3 ( x ) = x 2 4 p :

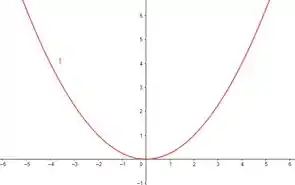
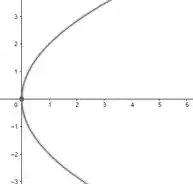
Passo 2

Encontrando as interseções, teremos:

  1. Curva 1 e 3:

    2. f 1 x = f 3 x → 4 p x = x 2 4 p → ^ 2 x 4 = 64 p 3 x → x = 4 p → A = 4 p , 4 p   e   B = ( 0,0 )

  2. Curva 2 e 3:

f 2 x = f 3 x → - 4 p x = x 2 4 p → ^ 2 L a d o   d i r e i t o ≤ 0   e   l a d o   e s q u e r d o ≥ 0 → B = ( 0,0 )

Passo 3

Analisando o gráfico, e considerando p ≥ 0 , teremos que o gráfico será:

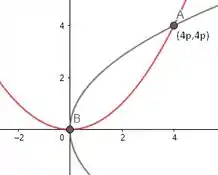
Daí, teremos que:

A = ∫ f x d x ,   o n d e   f x = f 1 x - f 3 x →

A = ∫ 0 4 p 4 p x - x 2 4 p d x = 2 3 4 p x 3 - x 3 12 p 4 p 0 → 2 3 4 p ( 4 p ) 3 - ( 4 p ) 3 12 p - 0 →

A = 32 p 2 3 - 16 p 2 3 = 16 p 2 3   u . a .

Passo 4

Derivando A em função de p, temos que:

A ' p = d A d p = 32 p 3 → A ' 3 = 32

Resposta

Logo, a taxa de variação é 32.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = ln ⁡ x ,y = 0ex = 4
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = 1 - x 2ey = - 3
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = x 3 - xey = 0
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = cos ⁡ xey = - cos ⁡ x ,x ∈ - π 2 , 3 π 2
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. x = y 3ex = y