Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 35

Ache o volume do sólido gerado pela rotação, em torno da reta x = 3 , da região limitada por aquela reta, pelo eixo x e pelo gráfico y = 9 x - x 4 12 .

Passo 1

Pessoal, como vai ser a rotação em torno da reta x = 3 paralela ao eixo y e temos uma função na variável x , está perfeito para usarmos o método das cascas cilíndricas, ok?

Agora para resolver, a primeira coisa a se fazer é lembrar a fórmula que calcula o volume sólido obtido pela rotação da região limitada por uma função em um intervalo [ a ,   b ] .

V = 2 π ∫ a b r x h ( x ) d x

Aqui temos que tomar cuidado pois a rotação é em torno do eixo x = 3 , nesse caso, o r x = 3 - x e nossa h x = f ( x ) = 9 x - x 4 12 , pois será a área entre ela e o eixo x . O intervalo de integração será de 0 a reta x = 3 . Sendo assim, o volume é dado por:

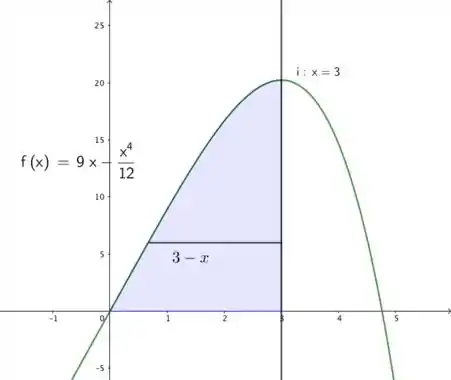
V = 2 π ∫ 0 3 ( 3 - x ) 9 x - x 4 12 d x = 2 π ∫ 0 3 x 5 12 - x 4 4 - 9 x 2 + 27 x d x

Vamos confirmar olhando a figura da região abaixo:

Passo 2

Já podemos resolver a integral. Sabemos da integral definida que

∫ a b f x d x = F b - F a

Em que F é uma primitiva de f .

Devemos lembrar também que:

∫ x n d x = x n + 1 n + 1 + C           n ≠ - 1

Dessa forma,

V = 2 π ∫ 0 3 x 5 12 - x 4 4 - 9 x 2 + 27 x d x = 2 π x 6 6 ⋅ 12 - x 5 5 ⋅ 4 - 9 x 3 3 + 27 x 2 2 0 3

= 2 π ( 3 ) 6 72 - ( 3 ) 5 20 - 3 ( 3 ) 3 + 27 ( 3 ) 2 2 - ( 0 ) 6 72 - ( 0 ) 5 20 - 3 ( 0 ) 3 + 27 ( 0 ) 2 2

= 2 π 729 72 - 243 20 - 81 + 243 2 = π 729 36 - 243 10 - 162 + 243

= π 81 4 - 243 10 + 81 = π 5 ⋅ 81 - 2 ⋅ 243 + 20 ⋅ 81 20 = π 20 405 - 486 + 1620

= 1539 π 20   u . v

Logo, o volume é V = 1539 π 20   u . v .

Resposta

V = 1539 π 20   u . v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada integral representa o volume de um sólido. Descreva o sólido. ∫ 0 1 2 π ( 3 - y ) ( 1 - y 2 ) d y
Cada integral representa o volume de um sólido. Descreva o sólido. ∫ 0 3 2 π x 5 d x