Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 32
Use o teorema de Pappus para encontrar o volume de um cone circular reto com 2 m de raio da base 3 m de altura.
Passo 1
Vamos lembrar qual o enunciado do teorema de Pappus: Se uma região plana girar em torno de uma reta em seu plano que não corta a região, então, a medida do volume do sólido de revolução gerado será igual ao produto da medida da área pela medida da distância percorrida pelo centróide da região.
Então teríamos a fórmula para o volume como sendo .
Agora devemos perceber que esse cone é obtido quando fazemos a revolução de um triângulo reto de base 2 m e altura 3 m em torno do eixo , por exemplo. Segue a figura:
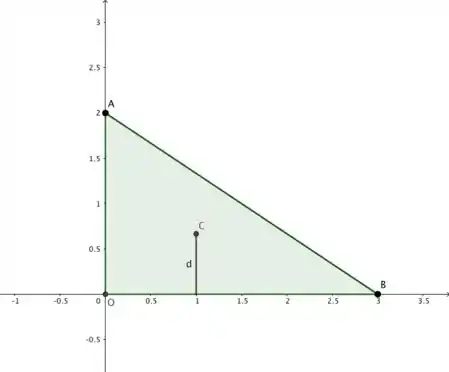
Pela fórmula do teorema de Pappus, o volume da esfera seria:
Lembre-se que a área do triângulo e perceba que é a distância percorrida pelo centróide quando fazemos a revolução dessa região em torno do eixo (é o comprimento da circunferência de raio ). Então para calcular esse volume, vamos precisar agora da ordenada do centróide, que tem comprimento .
Passo 2
Agora devemos achar o centróide, que, no caso do triângulo, é o seu baricentro . Temos a seguinte fórmula para o baricentro do triângulo de vértices e :
Sendo assim, .
Passo 3
Acabamos de descobrir que , então, o volume é:
Prontinho.