Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 29

Cada integral representa o volume de um sólido. Descreva o sólido.

∫ 0 3 2 π x 5 d x

Passo 1

Fala aí! Tudo certinho? 😬

Nesse problema foi dada uma integral definida e nosso objetivo é basicamente descrever o volume do solido que é formado por ela.

Parece complicado? 👀

Primeiro vamos reescrever a nossa integral da seguinte maneira

∫ 0 3 2 π x 5 d x = 2 π ∫ 0 3 x ( x 4 ) d x

Essa disposição da integral te lembra alguma coisa? Nenhum método de integral de revolução?

Veja só! 😉

Passo 2

Podemos perceber que o sólido é obtido pela rotação da região 0 ≤ y ≤ x 4 , 0 ≤ x ≤ 3 sobre o eixo y usando cascas cilíndricas.

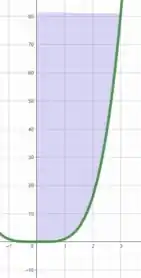
Isso porque para cada valor de x no intervalo 0,3 , estamos multiplicando 2 π x que faz papel do comprimento de circunferência vezes x 4 que faz o papel da altura.

Ao somar (no caso, integrar) tudo isso temos a rotação da curva 0 ≤ y ≤ x 4 no intervalo 0 ≤ x ≤ 3 em torno do eixo y .

Portanto, o volume gerado pela integral do enunciado é o volume do solido de revolução limitado pela area entre y = x 4 e y = 0 com x variando entre 0 e 3 .

E aí! O que achou? Responde Aí! 😉

Resposta

O volume gerado pela integral do enunciado é o volume do solido de revolução limitado pela area entre y = x 4 e y = 0 com x variando entre 0 e 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1 – 12. Resolva os Exercícios de 5 a 16 da seção 6.1 pelo método do invólucro cilíndrico.Nos Exercícios, ache o volume do sólido de revolução gerado pela rotação, em torno da reta indicada, da região
Na Figura abaixo, a região limitada pelo eixo x, pela reta x = 1 e pela curva y = x 2 é denotada por R1; a região limitada pelas curvas y = x 2 e y 2 = x é denotada por R2; a região limitada pelo eixo
Um sólido de revolução é formado quando a região limitada pela curva y = x 3 , pelo eixo x e pela reta x = c ( c0 ) gira em torno do eixo y . Tome os elementos de área retangulares paralelos ao eixo d
Ache o volume do sólido gerado pela rotação da região fora da curva y = x 2 e entre as retas y = 2 x - 1 e y = x + 2 em torno do eixo y .
Ache o volume do solido gerado por rotação, em torno do eixo x da região limitada pela curva y = x 4 , a reta x= 1 e eixo x