Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.7 - Ex. 30

Determine o valor exato de ∫ ∫ S x 2 y z   d S , onde S é a superfície do Exercício 29.

Passo 1

Fala, turma! Como estão?

A questão pede o valor de

∫ ∫ S x 2 y z     d S

Com precisão de até 4 casas decimais. No livro temos o símbolo ao lado dessa questão, o que significa que vamos precisar usar um software ou calculadora para obter o valor dessa integral. Podemos usar o software WolframAlpha. E para isso falta determinarmos nossos limites de integra��ão e calcular nosso termo:

d S = d z d x 2 + d z d y 2 + 1   d x d y

A superfície do exercício 29 é:

z = x y ,   0 ≤ x ≤ 1 ,   0 ≤ y ≤ 1

Bora lá!

Passo 2

Com os dados que nos foram fornecidos, podemos calcular o jacobiano dessa superfície da seguinte forma:

d S = d z d x 2 + d z d y 2 + 1   d x d y

O enunciado traz que S é a superfície:

z = x y

Calculando suas derivadas parciais. Derivando em x , tratando y como constante:

d z d x = d x y d x = y

Derivando em y , tratando x como constante:

d z d y = d x y d y = x

Então, substituindo na equação de d S :

d z d x 2 + d z d y 2 + 1   d x d y = y 2 + x 2 + 1   d x d y

Passo 3

O enunciado traz o intervalo das nossas variáveis:

0 ≤ x ≤ 1

  0 ≤ y ≤ 1

Podemos substituir no nosso integrando:

z = x y

Então, nossa integral completa é:

∫ ∫ S x 2 y z   d S = ∫ 0 1 ∫ 0 1 x 2 y x y y 2 + x 2 + 1   d x d y

Multiplicando:

∫ 0 1 ∫ 0 1 x 3 y 2   y 2 + x 2 + 1   d x   d y

Passo 4

Utilizando o WolframAlpha nós encontramos a seguinte resposta para esse problema.

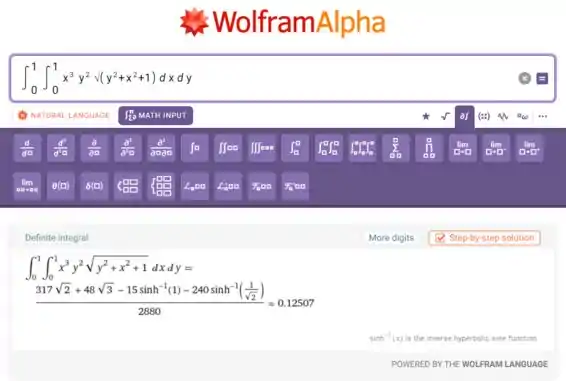
Com quatro casas decimais isso fica:

∫ 0 1 ∫ 0 1 x 3 y 2   y 2 + x 2 + 1   d x   d y ≈ 0,1251

Resposta

∫ 0 1 ∫ 0 1 x 3 y 2   y 2 + x 2 + 1   d x   d y ≈ 0,1251

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a lei de Gauss para achar a carga contida no hemisfério sólido x 2 + y ² + z ² ≤ a 2 ,z ≥ 0 ² ² , se o campo elétrico for E → x , y , z = x i → + y j → + 2 z k →
Seja F → um campo inverso do quadrado, ou seja F → r = c r → / | r → | ³ ³ para alguma constante c , onde r = x i → + y j → + z k → . Mostre que o fluxo de F → por uma esfera S com centro na origem é
Use a lei de Gauss para achar a carga dentro de um cubo com vértices ( ± 1 ,± 1 , ± 1 ) se o campo elétrico for E → x , y , z = x i → + y j → + z k →
Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F → através de S . Para superfícies fechadas, use a
Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F através deS . Para superfícies fechadas, use a ori