Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.7 - Ex. 32
Determine o fluxo de através da parte do cilindro que está acima do plano e entre os planos e com orientação para cima. Ilustre, usando um sistema algébrico computacional para desenhar o cilindro e o campo vetorial na mesma tela.
Passo 1
Oii, pessoal! Tudo certo?
A questão pede o fluxo do campo vetorial:
Através da parte do cilindro:
que está acima do plano e entre os planos e com orientação para cima.
Para calcular o fluxo do campo vetorial, temos a integral dupla:
Como estamos lidando com o gráfico de uma função:
Podemos escrever nossa função em função de :
E calcularmos nossa integral de linha pela equação:
Aqui, , , são as componentes da nossa função campo:
Então, vamos precisar achar as derivadas parciais:
E:
E substituímos na nossa equação. Depois é só calcularmos a integral dupla como já estamos acostumados.
A questão também pede para desenharmos por um software o cilindro e o campo vetorial na mesma tela. Para isso podemos usar o GeoGebra. Vamos lá!
Passo 2
A função é a função , onde no caso dessa questão pode ser encontrada pela equação do cilindro e que será igual a:
Tirando a raiz dos termos:
A função campo tem formato:
Retomando a equação do campo dada pelo enunciado:
Então, nossos termos , , são:
Calculando as derivadas parciais:
- Derivando em , tratando como constante:
- Derivando em , tratando como constante:
Passo 3
Vamos substituir esses termos na nossa equação:
Nosso primeiro termo vai zerar e rearranjando os termos, ficaremos com:
Pensando nos limites de integração, o enunciado traz que: a superfície está entre os planos e . Então:
Fazendo , temos nossa superfície no plano :
Elevando a equação ao quadrado:
Isolando :
Tirando a raiz quadrada:
Então os limites são:
Passo 4
Isso nos deixa com a integral igual a:
Utilizando o CAS para integral a primeira função nós conseguimos como resposta:
E para a segunda:
Dessa forma a reposta exata disso é:
Passo 5
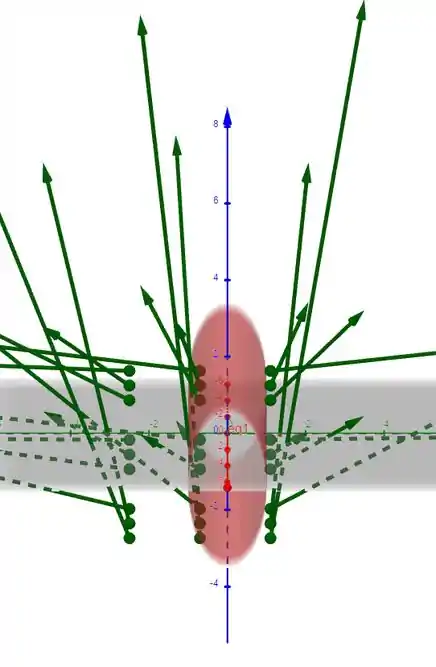
Aqui, usamos o GeoGebra para plotar o campo vetorial e o cilindro. Para o cilindro, basta colocar a função:
Para o campo vetorial, usamos a função sequência do software e digitamos o vetor:
E variamos os valores de , e livremente. Isso nos dá a imagem:
