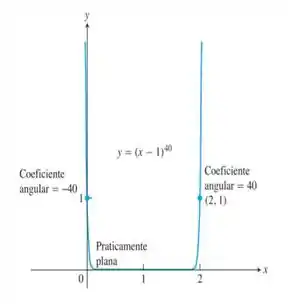
Algumas curvas são tão planas que, na prática, o método de Newton para demasiado longe da raiz para fornecer uma estimativa útil. Tente usar o método de Newton em com uma estimativa inicial de para verificar o quanto a sua calculadora se aproxima da raiz . Veja o gráfico a seguir.

Primeiramente, vamos derivar a função para, então, substituirmos na fórmula acima

Substituindo os valores de e vamos obter

Tomando, então, vamos obter

Repetindo esse procedimento, vamos perceber que a cada iteração a diferença entre os termos vai se tornando cada vez menor e não se aproximam de 1 rapidamente como, por exemplo, que é maior que 1 (raiz exata).