Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.5 - Ex. 7
Algumas vezes uma solução de equilíbrio constante tem a propriedade de que soluções de um lado da solução de equilíbrio tendem a se aproximar dela, enquanto soluções do outro lado tendem as e afastar (veja a Figura2.5.9). nesse caso, a solução de equilíbrio é dita semiestável.
(a) Considere a equação
em que é uma constante positiva. Mostre que é o único ponto crítico correspondendo à solução de equilíbrio .
(b) Esboce o gráfico de em função de . mostre que é uma função crescente de para e para . A reta de fase tem setas apontando para cima tanto abaixo quanto acima de . Assim, soluções abaixo da solução de equilíbrio aproximam-se dela, enquanto as soluções acima se afastam dela. Portanto, é semiestável.
(c) Resolve a equação sujeita à condição inicial , e confirme as conclusões do item (b).
Passo 1
Vamos responder as duas letras (a) e (b) juntas usando um gráfico com várias soluções, a função que estamos usando é:
O gráfico então vai ser, usando (qualquer k é válido desde que seja positivo):
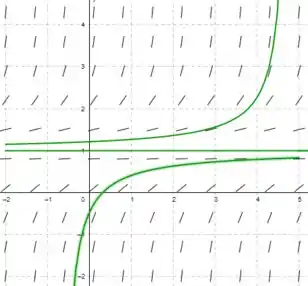
Como dá para ver, o único ponto de equilíbrio está em , as soluções vizinhas se aproximam se e se afastam
Passo 2
c) A equação diferencial é separável, vamos então primeiro separar os termos diferenciais:
Integrar dos dois lados:
E isolar :
Substituindo a condição inicial :
Tirando MMC:
Reescrevendo:
Tirando fator comum:
E isolando :
A solução passa a ser:
Reorganizando:
Resposta
Ei, a resposta está no passo a passo :)