Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 7
As alturas de onda em mar aberto dependem da velocidade do vento e do tempo que o vento tem soprado a essa velocidade. Os valores da função , td estão registrados nos pés na Tabela .
- Qual é o valor de ? O que isso significa?
- Qual o significado da função ? Descreva o comportamento dessa função.
- Qual o significado da função ? Descreva o comportamento dessa função.
Passo 1
Vamos resolver essa atividade juntos meu querido estudante.
A gente tem que as alturas das ondas se relacionam com a velocidade e o tempo e uma função:
Os valores dessa relação estão na tabela:
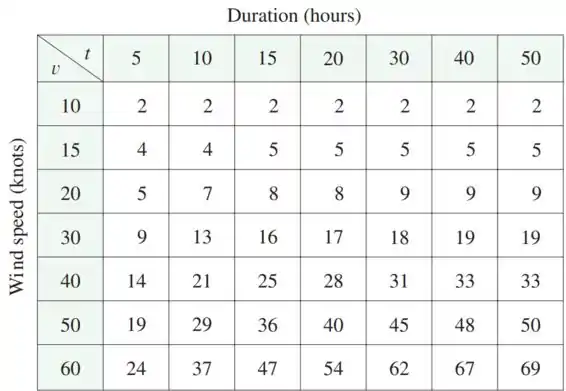
Primeiramente, é importante entender o que significa .
A expressão mostra que a altura das ondas depende da velocidade do vento e do tempo de duração do vento.
Logo, basta procurar pelos valores de e na tabela, para se achar .
Passo 2
- .
Basta ver o valor na tabela que é o encontro da linha e da coluna .
O significado dessa função é que com um vento de 80 Km/h soprando em mar aberto por 15 horas, há uma formação de ondas de 7,7 metros de altura.
Passo 3
b) .
A função retorna a altura das ondas produzidas por um vento de 60 km/h soprando em mar aberto por horas.
Olhando os valores na tabela, percebe-se que com o aumento de , aumenta .
Passo 4
c) .
A função retorna a altura das ondas produzidas por um vento de velocidade soprando em mar aberto por 30 horas.
Olhando os valores na tabela, percebe-se que com o aumento de , aumenta .
Resposta
a)
b) . A função retorna a altura das ondas produzidas por um vento de 60 km/h soprando em mar aberto por horas.
c) . A função retorna a altura das ondas produzidas por um vento de velocidade soprando em mar aberto por 30 horas.