Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.3 - Ex. 29

29- Aproxime o comprimento do arco de um quarto de círculo unitário ( que é π / 2 ) pelo cálculo do comprimento da aproximação poligonal com n = 4 segmentos (veja a figura a seguir).

Passo 1

A equação de um circunferência pode ser escrita como:

x 2 + y 2 = r 2

Onde a nossa circunferência tem raio 1, e como somente temos os valores de x precisamos descobrir os valor de y para isso precisamos isolar y na equação.

y = 1 - x 2

Para x = 0 :

y = 1 - 0 2 = 1

Para x = 0.25 = 1 4 :

y = 1 - ( 0.25 ) 2 = 15 4

Para x = 0 . 5 = 1 2 :

y = 1 - ( 0.5 ) 2 = 3 2

Para x = 0 . 75 = 3 4 :

y = 1 - ( 0 . 75 ) 2 = 7 4

Para x = 1 :

y = 1 - 1 2 = 0

Passo 2

Por geometria analítica temos que a distância entre dois pontos A e B que formam uma reta é:

d A B = y b - y a 2 + x b - x a 2

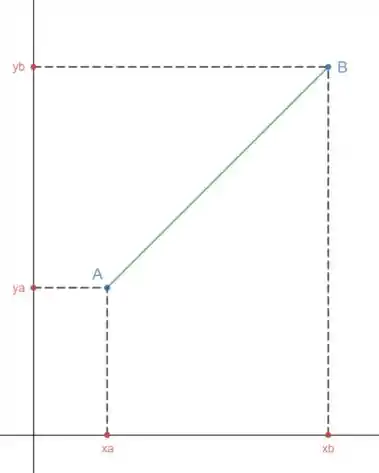
Com a tabela dos pontos encontrados no passo 1 podemos escrever a somatória das distâncias:

Passo 3

L = 0.25 - 0 2 + 15 4 - 1 2 + 0.5 - 0.25 2 + 3 2 - 15 4 2 + 0.75 - 0.5 2 + 7 4 - 3 2 2   + 1 - 0.75 2 + 0 - 7 4 2

L = 0.252 + 0.27 + 0.323 + 0.707 = 1.552

Resposta

1.552

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ e ∞ 1 xln ⁡ x 3d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 0 + ∞ e x e 2 x + 3d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ - ∞ + ∞ x 2 9 + x 6d x
Ache o comprimento exato da curva. 36 y 2 = x 2 - 4 3 2 ≤ x ≤ 3 ,y ≥ 0
Use a fórmula do comprimento de arco para achar o comprimento da curva y = 2 - x 2 , 0 ≤ x ≤ 1 . Verifique o seu resultado observando que a curva é um quarto de círculo.