Exercícios de Comprimento de Arco - Lista de Exercícios Resolvida

Ache o comprimento da curva:

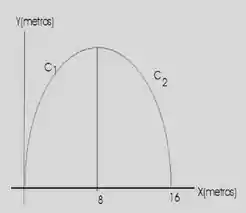
A entrada de um dos estádios para as Olimpíadas de 2016 tem a forma da figura abaixo, e é constituída por 2 tubos circulares na forma de arco de curvas e , iluminados internamente com as cores dos países participantes. O custo estimado para estes tubos é de por metro. A curva é determinada por: e a curva por: . Determine o custo total desta obra.

Ache o comprimento do arco da curva do ponto ao ponto .

Calcule o comprimento do arco enunciado abaixo:

Calcule o comprimento de para

Calcule o comprimento de

em .

O comprimento do gráfico de no intervalo é:

Calcule o comprimento de arco da curva entre os pontos e .

Consideremos a espiral . Determinar o comprimento desta curva para como função de . Calcular . Determinar de tal maneira que .

Determine o comprimento das curvas abaixo:

1. A parábola
2. O cardioide

O comprimento da curva , é

Decida se cada uma das afirmações abaixo é verdadeira ou falsa.

1. Se é derivável com derivada contínua e , para todo Então, o comprimento do gráfico de é, no mínimo,

2. Se são contínuas e então

3. Se é uma função contínua e ímpar então qualquer primitiva de é par.

4. Se é contínua então existe tal que .

Monte a integral que calcula o comprimento de arco em cada um dos casos; quando possível, resolva a integral

Monte a integral que calcula o comprimento de arco em cada um dos casos; quando possível, resolva a integral

Monte a integral que calcula o comprimento de arco em cada um dos casos; quando possível, resolva a integral

Monte a integral que calcula o comprimento de arco em cada um dos casos; quando possível, resolva a integral

Monte a integral que calcula o comprimento de arco em cada um dos casos; quando possível, resolva a integral

Calcule o comprimento de arco do gráfico de , desde o ponto até .

Calcule o comprimento de arco do gráfico da função

De até

Considere o triângulo curvilíneo cujos lados são:

• O gráfico de para
• O segmento de reta que liga os pontos e
• E o arco de círculo de centro e raio , que tem

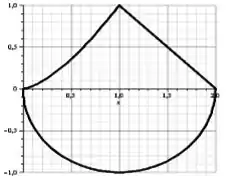
Escreva as três integrais que permitem calcular os comprimentos dos três lados do triângulo curvilíneo.

Determine o perímetro do triângulo curvilíneo.

O comprimento da curva para é:

a)

b)

c)

d)

e)

O comprimento da curva para é:

a)

b)

c)

d)

e)

O comprimento da curva para é:

a)

b)

c)

d)

e)

Calcule o comprimento do gráfico de em .

Monte a integral que calcula o comprimento de arco em cada um dos casos; quando possível, resolva a integral

Monte a integral que calcula o comprimento de arco em cada um dos casos; quando possível, resolva a integral

Calcule o comprimento de para

Seja

Determine a derivada da função .

Seja a inversa de . Determine .

Ache o comprimento da parte do gráfico de compreendido entre os pontos e .

4) O comprimento do gráfico de para vale:

Sabendo que o comprimento de onda de uma curva lisa , é dada pela fórmula:

Encontre o comprimento da curva , .

Seja:

Ache o comprimento da parte do gráfico de compreendido entre os pontos e .

Calcule o comprimento do arco de curva sobre o intervalo

sobre

O comprimento da curva para é:

a)

b)

c)

d)

e)

Determine o comprimento de arco da curva..

Calcule o comprimento do arco de curva sobre o intervalo

sobre

Uma estrada é construída ligando o ponto ao ponto seguindo a trajetória da parábola

Calcule o comprimento dessa estrada.

21) As coordenadas do centro de gravidade de um arco de curva (homogêneo) são dadas por

Em que é o comprimento do arco. Calcule as coordenadas do centro de gravidade dos arcos abaixo:

1. Arco da catenária para

21) As coordenadas do centro de gravidade de um arco de curva (homogêneo) são dadas por

Em que é o comprimento do arco. Calcule as coordenadas do centro de gravidade dos arcos abaixo:

1. Arco de circunferência de raio subtendo o ângulo

Calcule o comprimento das curvas

Calcule o comprimento das curvas

a)

Calcule o comprimento das curvas

Calcule o comprimento das curvas

Calcule o comprimento das curvas

Dê uma parametrização para a curva dada pela interseção das seguintes superfícies:

Determine o comprimento das curvas abaixo:

1. A parábola
2. O cardioide

Calcule o comprimento das curvas:

Mostre que o comprimento da curva em qualquer intervalo é igual ao valor da área da região limitada pela curva.

Calcule o comprimento das curvas:

Seja . Mostre que , para todo .

Calcule o comprimento das curvas

Encontre o ponto da curva espacial

situado a uma distância de unidades ao longo da curva a partir do ponto na direção do comprimento de arco crescente.

Em cada item, encontre o comprimento de arco descrito por uma partícula em movimento sobre uma curva de acordo com a equação dada, durante o intervalo de tempo dado em cada caso.

Calcule o comprimento de arco da curva , onde .

Calcule os limites abaixo:

f)

Calcule os limites abaixo:

g)

Em cada item, encontre o comprimento de arco descrito por uma partícula em movimento sobre uma curva de acordo com a equação dada, durante o intervalo de tempo dado em cada caso.

Em cada item, encontre o comprimento de arco descrito por uma partícula em movimento sobre uma curva de acordo com a equação dada, durante o intervalo de tempo dado em cada caso.

Calcule os limites abaixo:

j)

Em cada item, encontre o comprimento de arco descrito por uma partícula em movimento sobre uma curva de acordo com a equação dada, durante o intervalo de tempo dado em cada caso.

Establecer integrais para os comprimentos das curvas cujas equações são

Estabelecer a integral que dá o comprimento da curva desde x = 0 até x = a, onde a > 0 e c > 0.

Prove que o produto do comprimento desta curva vezes c é igual a área da região limitada por , o eixo X, o eixo Y e a reta x = a.

Demonstrar que o comprimento da curva que une os pontos e é se .

Calcule os limites abaixo:

m)

Calcule os limites abaixo:

n)

Establecer integrais para os comprimentos das curvas cujas equações são

Em cada item, encontre o comprimento de arco descrito por uma partícula em movimento sobre uma curva de acordo com a equação dada, durante o intervalo de tempo dado em cada caso.

d)

Utilizando a equação vetorial onde , provar que o comprimento L de uma elipse está dada pela integral

onde . O número é a excentricidade da elipse. Este é um caso particular de uma integral da forma:

chamada integral elíptica de segunda classe, onde . Os números estão tabulados para vários valores de .

Calcule (atenção: não é permitido usar derivadas no cálculo dos limites!):

(c)

Calcule o comprimento das curvas:

Calcule o comprimento das curvas:

Calcule o comprimento das curvas dadas no intervalo dado:

a) ,

Calcule o comprimento das curvas dadas no intervalo dado:

c) ,

Se comprimento do gráfico de para é

Então

1. .
2. .
3. .
4. .

O comprimento da curva para é:

a)

b)

c)

d)

e)

Seja . Calcule o comprimento da curva de à .

Em cada item, encontre o comprimento de arco descrito por uma partícula em movimento sobre uma curva de acordo com a equação dada, durante o intervalo de tempo dado em cada caso.

Calcule (atenção: não é permitido usar derivadas no cálculo dos limites!):

(b)

Em cada item, encontre o comprimento de arco descrito por uma partícula em movimento sobre uma curva de acordo com a equação dada, durante o intervalo de tempo dado em cada caso.

Calcule esta integral e encontre o comprimento da curva quando a = 2.

Calcule o comprimento da curva dada em coordenadas polares.

c)

Calcule o comprimento da curva dada em coordenadas polares.

d)

Consideremos a curva para .

a) Determinar o comprimento desta curva.

Determinar em o comprimento da curva

Calcule o comprimento do arco de curva sobre o intervalo

sobre